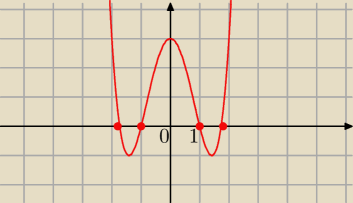
Nierówność wielomianowa Witam: Witam mam problem z rozwiązaniem takiej nierówności wielomianowej: x⁴ −4x² ≥−3 wiem że trzeba dodać do obu stron 3 a potem użyć róznych wzorów, ale wychodzą mi inne wyniki niż w odpowiedziach Odpowiedź jest równa (−∞, −√3> u <−1,1> u <√3, +∞)

ABC: x⁴−4x²+3≥0 (x²−1)(x²−3)≥0 (x−1)(x+1)(x−√3)(x+√3)=0 i metoda wężyka wszystkie pierwiastki pojedyńcze nigdzie się nie odbija tylko zawsze na drugą stronę

janek191:

ABC:

Witam: Dziękuje, wykres i resztę to umiem i rozumem tylko nie wiem jak przejść z x⁴−4x²+3≥0 do (x²−1)(x²−3)≥0

ABC: możesz tak x⁴−x²−3x²+3=x²(x²−1)−3(x²−1)=(x²−1)(x²−3)

janek191: W pamięci lub t = x² x⁴ = t² Mamy t² − 4 t + 3 ≥ 0 Δ = 16 − 12 = 4 √Δ = 2

	4 − 2		4 + 2
t =		= 1 lub t =		= 3
	2		2

( t − 1)*( t − 3) ≥ 0 ( x² − 1)*( x² − 3) ≥ 0

Bleee: Mozesz też zrobić podstawienie: t = x² I wtedy masz: t² − 4t + 3 ≥ 0 Δ i te sprawy

Witam: Ok czyli że trzeba rozbić poszczególne składniki w taki sposób by były podobne, ok rozumiem, dziękuje

Bleee: Ogólnie także warto wyrobić sobie odruch sprawdzania czy 1 lub − 1 jest pierwiastkiem bo ogranicza się to sumowania (odejmowaniu) współczynników przy kolejnych potegach.