Jednokładnosc pomocy Mortis: W jednokładności J^k s obrazem okregu o₁ i rwaniu (x−3)²+(y−4)²=1 jest okrąg o₂ o środku O₂ i równaniu (x+3)² + (y+2)² = 16. Oblicz współrzędne środka jednokładności, jeśli skala k jest liczba dodatnia

Mortis: pomoze ktoś?

student: https://zadania.info/d401/4580233

Kuba: o1: (x−3)²+(y−4)²=1 ⇒ S1=(3;4) r1=1 o2: (x+3)²+(y+2)²=16 ⇒ S2=(−3;−2) r2=4 Skale k obliczam dzięki znajomości długości dwóch odcinków w tym przypadku promieni

	r2
k2=		k2=4:1 k2=4 k=2 v k=−2 Odrzucam rozwiązanie k=−2 gdyż w zadaniu k>0
	r1

ze wzoru x`=x(k)+(1−k)a y`=y(k)+(1−k)b otrzymam środek jednokładności S=(a;b) podstawiam do wzoru dla x −3=3(2)+(1−2)a analogicznie postępuje z y po wykonaniu obliczeń o ile się nie pomyliłem otrzymuje S=(9;10)

SK:

r1
	= |k|
r2

S: Kuba źle!

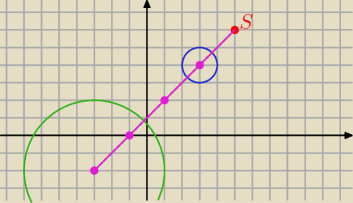
a@b: o₁: (x−3)²+(x−4)²=1 , O₁(3,4) r₁=1 o₂ : (x+3)²+(y+2)²=16 , O₂(−3,−2), r₂=4

r2
	=|k| i w zad . k>0 ⇒ k=4
r1

S( x_S, y_S) −− środek jednokładności to → → SO₂=k*SO₁ [x_S+3, y_S+2]=4*[x_S−3, y_S−4] x_S+3=4x_S−12 i y_S+2=4y_S−16] 3x_S=15 i 3y_S=18 x_S= 5 i y_S=6 S(5,6) i k=4 ===========

a@b: J jak Mortis ? zakumałeś ? czy straciłeś .. głos ?

Mortis: A jakby to podstawić do ogl wzoru?