twierdzenie sinusów
salamandra:
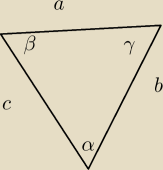
Twierdzenie sinusów: Rozwiąż trójkąt ABC w którym boki b i c mają odpowiednio długości 10 i 11
a kąt β ma miarę 30 stopni.
Wynik zaokrąglij do całości.
No i tu pojawia się problem o który pytałem w poście pare godzin temu, gdzie odpowiedzi nie
uzyskałem.
Mam tak:
10*sinγ = 5,5
sinγ = 0,55
γ≈34
α≈116
α≈116
β=30
γ≈34
I tu bym zakończył, ale w odpowiedzi jest jeszcze drugie rozwiązanie? Jak do niego dojść i
jakie są warunki, aby istniało to drugie rozwiązanie?
15 sty 20:27
Tess: Możesz mieć inny y.
2 siny w dziedzinie mają wartość 0,55
15 sty 20:36
Saizou :
sin γ =0,55
To równanie ma 2 rozwiązania w przedziale (0, 180)
15 sty 20:38
salamandra: Aaa, no to teraz rozumiem, bo sin34 to może być sin(180−34) czyli de facto γ może być 146?
15 sty 20:40
Saizou : Tak
15 sty 20:46
salamandra: Rozumiem, że nie muszę tego sprawdzać wtedy, gdy zalozmy hipotetycznie− bede miał podany kąt 70
stopni, drugi wyjdzie jakiś załóżmy 30 stopni, to drugiego przypadku nie będzie, ponieważ
jakby wziąć ten drugi przypadek z 30, to byłoby 150 stopni, i wtedy 150+70>180 i jest
sprzeczność tak?
15 sty 20:48
Saizou : Lepiej się uczyć że trzeba sprawdzić oba warianty, najwyżej w jednym wyjdzie sprzeczność
15 sty 20:52
salamandra: Potrafiłbyś z głowy podać takie dane, żeby wyszło jedno rozwiązanie, ale żebym sobie dla
przećwiczenia sprawdził?
15 sty 20:53
salamandra: Byłbym wdzieczny
15 sty 20:53
Mila:
Rozwiąż trójkąty mając dane:
Zadanie1.
a=8,c=16 ,∡β=600
zadanie 2.
a=2√2,b=3−√3, c=3√2
zadanie 3
a=2√3,b=6,∡A=30o ( dwa rozw.)
15 sty 22:41
salamandra: 1−sze nie lepiej z tw. cosinusów?
15 sty 23:12
salamandra: b2=64+256−2*8*16*cos60
b2 = 320−128
b2=192
b= 8√3
15 sty 23:15
salamandra: A ok, widzę, że i to i to
mając b, liczę α z tw. sinusów
α= 30 v α = 150 stopni − sprzeczność, bo 150+60 > 180
α=30
β=60
γ=180−(60+30) = 90
15 sty 23:21
salamandra: W 2−gim wychodzi mi w ogóle sprzeczność, że z tw. cosinusów, cosinus jest poza przedziałem
<−1;1>
15 sty 23:29
a@b:
2/ zawsze na początek sprawdź czy taki trójkąt istnieje
z warunku trójkąta
2√2+3−√3 >3√2
wniosek ......
15 sty 23:39
salamandra: No tak...

15 sty 23:41
salamandra: Pierwsze dobrze rozumiem?
15 sty 23:42
a@b:
Twierdzenie sinusów stosujemy w trójkącie ( który istnieje)
gdy mamy dane:
1/ dwa boki i kąt naprzeciw jednego z tych boków
lub 2/ dwa kąty i bok naprzeciw jednego z tych kątów
Twierdzenie cosinusów gdy mamy
1/ dwa boki i kąt między nimi
lub 2/ trzy boki
15 sty 23:50
a@b:
3/ trójkąta nie da się rozwiązać gdy mamy podane tylko dwa kąty
(to chyba już wiesz ? dlaczego?
15 sty 23:53
a@b:
Zapomniałam jeszcze dopisać w tw. sinusów
3/ gdy mamy dane R −− promień okręgu opisanego
i dwa boki
4/ lub R i dwa kąty
15 sty 23:55
a@b:
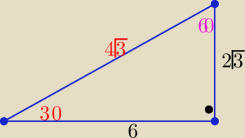
zad3/ jak widzisz dany kąt 30
o ( lub 60
o lub 45
o
to sprawdź ( może to trójkąt "ekierkowy " ?
pasuje

zatem trójkąt jest prostokątny ( jak na rysunku)
16 sty 00:00
a@b:
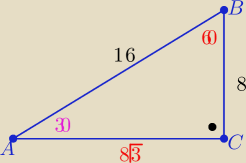
zad 1/
16 sty 00:05
Mila:
3) β=60o lub β=180o−60o=120o
16 sty 00:09
 Twierdzenie sinusów: Rozwiąż trójkąt ABC w którym boki b i c mają odpowiednio długości 10 i 11
a kąt β ma miarę 30 stopni.
Wynik zaokrąglij do całości.
No i tu pojawia się problem o który pytałem w poście pare godzin temu, gdzie odpowiedzi nie
uzyskałem.
Mam tak:
Twierdzenie sinusów: Rozwiąż trójkąt ABC w którym boki b i c mają odpowiednio długości 10 i 11
a kąt β ma miarę 30 stopni.
Wynik zaokrąglij do całości.
No i tu pojawia się problem o który pytałem w poście pare godzin temu, gdzie odpowiedzi nie
uzyskałem.
Mam tak:

 zad3/ jak widzisz dany kąt 30o ( lub 60o lub 45o
to sprawdź ( może to trójkąt "ekierkowy " ?
pasuje
zad3/ jak widzisz dany kąt 30o ( lub 60o lub 45o
to sprawdź ( może to trójkąt "ekierkowy " ?
pasuje zatem trójkąt jest prostokątny ( jak na rysunku)
zatem trójkąt jest prostokątny ( jak na rysunku)
 zad 1/
zad 1/