optymalizacja Heniu: Dany jest kwadrat o boku długości 4. Na bokach AB,BC,CD,DA umieszczono odpowiednio punkty K,L,M,N takie że AN=1, CM=2, BK=3BL. Oblicz pole czworokąta KLMN wiedząc, że wyrażenie KL² + LM² + MN² + NK² osiąga najmniejszą możliwą wartość.

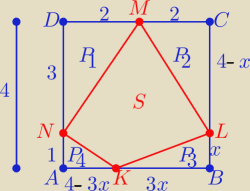
Eta: x ∊(0,4/3) S=P□−(P₁+P₂+P₃+P₄) P(x)=P₁+P₂+P₃+P₄

	3		3
P(x)= 3+4−x+		x2+2−		x
	2		2

.................. P(x)= 1,5x²−2,5x+9 −−− parabola ramionami do góry więc funkcja P(x) osiąga wartość najmniejszą w wierzchołku x_min= 2,5/3 = 5/6 to policz : P(5/6)= ...... −−−− wartość pola najmniejsza dokończ S= 16− P(5/6)=...... i po ptokach