Przebieg zmienności funkcji
Student001: Granice na krańcach określoności funkcji i asymptoty
lim−>∞ 2x2/x+3
O ile dobrze rozumiem i przy obliczeniach się nie pomyliłem to granice wynoszą −∞ i x=−3 jest
równaniem asymptoty pionowej obustronnej.
Ale mam problem z obliczeniem ukośnej/poziomej.
przy lim−>∞ 2x2/x+3 muszę zastosować metodę, tylko jaką?
Skoro pod wzór limx−>∞ (f(x)−ax) podstawię to wychodzi lim−>∞2x2/x+3 * 1/x+3 . Tutaj mnożenie
przez sprzężenie raczej odpada. Co więc zastosować?
14 sty 23:15
uczennica Kaja: | | 2x2 | |
Oryginalna funkcja to |
| ? Bo zapis jest niejasny |
| | x+3 | |
14 sty 23:49
Student001: Tak
15 sty 00:08
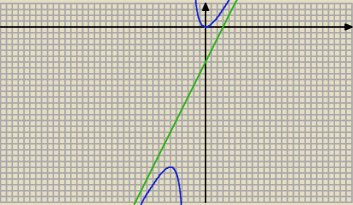
Maciess: Ukosna y=ax+b
| | f(x) | |
a=lim x−>∞ |
| (+− ∞ liczysz) |
| | x | |
b=lim x−>
∞(f(x)−ax)
Jesli granica jest niewłaściwa to asymptota nie istnieje
15 sty 07:56
piotr: a=2
b=−6
15 sty 11:03
piotr:
15 sty 11:06
