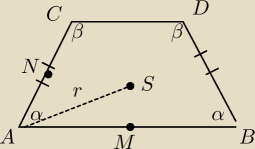
Okrąg opisany na czworokącie salamandra: Punkty A=(−4,2), B(2, −4), C= (3,1), D=(1,3) są wierzchołkami trapezu ABCD a) Uzasadnij, że na trapezie ABCD mozna opisac okrąg b) Napisz równanie okręgu opisanego na trapezie ABCD Proszę o sprawdzenie, ponieważ nie mam odpowiedzi, a wyszedł mi "dziwny" promień i środek a) 1. wyznaczam równanie prostej AB 2=−4a+b −4=2a+b −2=4a−b −4=2a+b 6a= −6 a=−1 b= 6 y= −x+6 2. wyznaczam równanie prostej CD 1=3a+b 3=a+b 1=3a+b −3=−a−b a= −1 b=4 y= −x+4 Jest to na pewno trapez, ponieważ ma jedną parę boków równoległych 3. Wyznaczam długości ramion AC i BD |AC| = √(3+4)²+(1−2)² = √50 |BD| = p{ (3−2)²+(3+4)² = √50 (nie mogę zrobić pierwiastka, bo robi się emotka, ale wiadomo o co chodzi) Odp a). Trapez jest równoramienny, więc można opisać na nim okrąg, gdyż suma przeciwległych kątów wynosi 180 stopni b)Wyznaczam punkt M, który leży w połowie boku |AB|

	−4+2		2−4
M=(		,		) = (−1, −1)
	2		2

Wyznaczam symetralną boku AB a = −1, więc a1 (współczynnik kierunkowy symetralnej) = 1 y=a(x−x0)+y0 − równanie prostej przechodzącej przez jeden punkt y=x+1−1 y=x Wyznaczam punkt N, który leży w połowie ramienia AC

	−4+3		2+1		−1		3
N=(		,		) = (		,		)
	2		2		2		2

Wyznaczam równanie prostej AC, gdyż wcześniej tego nie zrobiłem 1= 3a+b 2= −4a+b −1=−3a−b 2= −4a+b 1=−7a

	1
a= −
	7

Symetralna AC a1= 7

	1		3
y=7(x+		)+
	2		2

	7		3
y= 7x+		+		= 7x+5
	2		2

Punkt przecięcia symetralnych wyznaczy środek okręgu y=x y=7x+5 x=7x+5 −6x= 5

	5
x= −
	6

	5
y= −
	6

	5		5
S= (−		; −		)
	6		6

Odległość od środka do któregokolwiek wierzchołka równa się promieniowi np. |AS| = r

	5		5
|AS| = √		+4)2+(−		−2)2 (wszystko pod pierwiastkiem, znów jakis błąd)
	6		6

	19		−17		361		289
|AS| = √(		)2+(		)2 = √		+		(również wszystko pod
	6		6		36		36

pierwiastkiem) =

	650
√
	36

	650		325
r2 =		=
	36		18

równanie okręgu

	5		5		325
(x+		)2+(y+		)2 =
	6		6		18

Czy dobrze?

Szkolniak: Równanie prostej AB źle wyznaczone, y=−x−2

salamandra: No tak, chochlik, ale tutaj i tak to nic nie zmieni

Tadeusz: Napracowałaś się ... szacun ! Tyle, że długości boków możesz policzyć wprost ze wspłrzędnych wierzchołków

salamandra: W jaki sposób? Myślałem, że mogę tylko wtedy, gdy odcięta lub rzędna dwóch punktów jest taka sama, wtedy to wiadomo, np. A=(2,4), B=(2,6), to AB = 2, ale przy takich też?

Tadeusz: wzór na długość odcinka

salamandra: No to tak zrobiłem

Tadeusz: W treści masz napisane, że punkty są wierzchołkami trapezu nie musisz udowadniać

salamandra: Wiem, to miałem zrobić tylko tak o, dla przećwiczenia

janek191: B = ( 2, − 4) C = ( 3, 1) ISB I =I SC I ( S₁ = ( −1 , −1) S₂ = ( 2,2) y = x S = ( x, x) ( 2 − x)² + ( − 4 − x)² = ( 3 − x)² + ( 1 − x)² 4 − 4 x + x² + 16 +8 x + x² = 9 − 6 x + x² + 1 −2 x + x² 4 x + 20 = − 8 x + 10 12 x = − 10

	5
x = −
	6

więc

	−5
y =
	6

	5		5
S = (		,		)
	6		6

r² = I SC I²

	5		23		11		529
r2 = ( 3 +		)2 + (1+ U{5}6})2 = (		)2 + (		)2 =		+
	6		6		6		36

	121
		=
	36

	650
=
	36

Równanie okręgu

	5		5		325
( x +		)2 + ( y +		)2 =
	6		6		18

janek191: Przy S zgubiłem minusy