Powodzenia maturzyści - ćwiczcie!
Saizou :
Rozważmy trapez prostokątny ABCD o podstawach AB i CD oraz katach prostych
przy wierzchołkach A i D.
Wiedząc,że punkt S jest środkiem okręgu wpisanego w ten trapez oraz |SB|=4 i |SC|=2
Oblicz obwód trapezu ABCD
13 sty 17:18
Eta:
12
√5
====

13 sty 17:25
Saizou :
To zadanie od Ciebie
Eta z dawnych czasów

13 sty 17:29
Eta:
Co nagle, to po diable

Odp: L=7,2
√5
=========
13 sty 17:31
Eta:
Miło mi ,że jeszcze pamiętasz


13 sty 17:32
Saizou :
Co prawda, to prawda
Odpowiedź z 17:31 jest prawidłowa
13 sty 17:33
Eta:
Szkoda ,że teraz takich chętnych maturzystów ( jak kiedyś) brak

13 sty 17:34
Saizou : Z tego co widzę mamy na forum trzech
@Szkolniak, @salamandra i @Wolfik
13 sty 17:35
Eta: 
13 sty 17:36
Saizou : Dorzucę jeszcze to zadanie, też od Ciebie (na zachętę napiszę, że dwa razy je rozwiązywałem
i za każdym razem inaczej)
Oblicz pole trapezu, w którym suma kątów ostrych = 90o
zaś różnica kwadratów przekątnych jest równa 16
13 sty 18:00
salamandra:
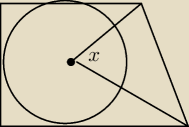
Odnośnie pierwszego.
Wybaczcie za rysunek, ale tylko mam pytanie, czy tam gdzie "x" będzie kąt prosty?
13 sty 18:18
Saizou :
Tak, tylko trzeba to uzasadnić
13 sty 18:19
salamandra: Jakaś wskazówka?
13 sty 18:27
Saizou :
Środek okręgu wpisanego w trapez to punkt przecięcia się dwusiecznych.
13 sty 18:29
salamandra: To wiem, ale stąd wynika że przy "x" będzie kąt prosty? Zaraz wyślę zdjęcie jaki rysunek
wykonałem, bo tutaj chyba nigdy nie nauczę się rysować

13 sty 18:31
Saizou : poprawiam treść zadania 2
W trapezie o kątach ostrych 30o i 60o, zaś różnica kwadratów przekątnych trapezu wynosi 16
Oblicz pole tego trapezu.
13 sty 18:32
Saizou :
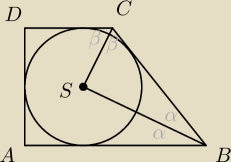
Ile wynosi suma miar kątów przy jednym ramieniu trapezu?
13 sty 18:34
salamandra:
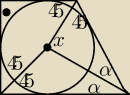
Ok, spróbuje tu:
2α+45+45 = 180
2α = 90
α = 45
więc kąt "x" to dopełnienie do 180, i jest prosty.
13 sty 18:45
salamandra: Zacząłem od wierzchołka A, skoro podzieli nam dwusieczna na 45 i 45, a przy wierzchołku D mamy
kąt prosty, to kąt przy wierzchołku C tego "małego" trójkąta po lewej będzie miał 45
Wiemy, że przy wierzchołku C, też jest dwusieczna, czyli drugi też musi mieć 45 stopni (przy
wierzchołku C), potem wiemy że suma kątów przy B i C musi dać 180 stopni, stąd 2α+90 = 180,
13 sty 18:47
Saizou :
Kąt przy wierzchołku C nie jest kątem prostym
13 sty 18:51
Saizou : Masz
2α+2β=180
α+β=90 stąd kąt CSB=90
13 sty 18:51
salamandra: No racja, na logike tam nie może byc 90 stopni, bo i czwarty musiałby tyle mieć, czyli cała ta
metoda do niczego?
13 sty 18:54
Saizou :
Ale co dalej? Pomyśl o polu ΔCSB i promieniu okręgu wpisanego w trapez
13 sty 18:56
salamandra: Pole CSB to oczywiście 4.
13 sty 19:00
Saizou : To teraz oblicz promień okrgeu
13 sty 19:14
salamandra: Mogę to zrobić nieznając α ani β?
13 sty 19:15
salamandra: Obliczyłem na razie CB = 2√5
13 sty 19:16
Saizou : Możesz

Równość pól
13 sty 19:27
Eta:
zad2
P=4√3
=======
13 sty 19:27
salamandra: chyba przerasta to moją wyobraźnie, przynajmniej na razie

13 sty 19:30
Saizou :
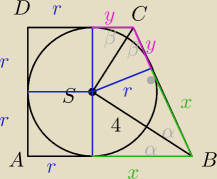
BC z Pitagorasa
| 1 | | 1 | |
| •|SC|•|SB|= |
| •r•|BC| stąd r |
| 2 | | 2 | |
Pitagoras dla x oraz y
13 sty 19:39
Eta:
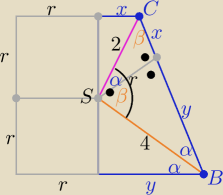
Obwód : 4r+2(x+y)
W ΔBCS : x+y=
√22+42= 2
√5
Obwód : L=...............
13 sty 19:39
Eta:

13 sty 19:40
salamandra: 1/2 * r * BC, który trójkąt w tym momencie liczysz, bo nie mogę się dopatrzeć?
13 sty 20:18
13 sty 20:31
salamandra: Bo promień to wysokość tego trojkata?
13 sty 20:37
Saizou : Tak

13 sty 20:45
salamandra:
4 =
√5*r
4
√5 = 5r
y
2+r
2 = 2
2
| | 4√5 | | 2√5 | | 8√5 | |
L = r+y+y+x+x+r+r+r = 4r+2x+2y = 4* |
| + 2* |
| +2* |
| = |
| | 5 | | 5 | | 5 | |
| | 16√5 | | 4√5 | | 16√5 | | 36√5 | |
= |
| + |
| + |
| = |
| ? |
| | 5 | | 5 | | 5 | | 5 | |
13 sty 21:05
Saizou :
i gites

13 sty 21:07
salamandra: W końcu..... twardy ten orzech (czyt. planimetria) dla mnie do przegryzienia....
13 sty 21:08
Saizou :
Trzeba ćwiczyć i ćwiczyć i ćwiczyć

13 sty 21:10
salamandra: Wiem, tak jak zapowiadałem, dziś miałem ostatni zawodowy i biorę się do roboty, mam nadzieję,
że nie jest za późno, zamierzam rozszerzenie na te 60% chociaż napisać... próbną napisałem na
44% teraz
13 sty 21:10
Saizou :
Łap zadanko
Kąt ostry równoległoboku mam miarę 60o. Odległość punktu przecięcia przekątnych
równoległoboku od jego boków są równa 2 i 1. Oblicz długości jego przekątnych .
13 sty 21:13
Saizou :
Z mojego doświadczenia, maturę rozszerzoną napisałem na 78%, a teraz skończyłem studia
z matematyki

Jak będziesz ćwiczyć to dasz radę.
13 sty 21:14
salamandra: Jeszcze rok temu nie wychodziłem poza 10%, jak sam od czasu do czasu zerknąłem. Takie rzeczy
jak parametry, czy cokolwiek związane z algebrą to robię z zamkniętymi oczami, ale geometria
od zawsze była moją pięta Achillesową i bez tego na rozszerzeniu nie da się osiągnąć dobrego
wyniku. Najgorsze, że w szkole jeszcze przede mną wiele materialu z geometrii− z planimetrii
jeszcze tw. sinusów/cosinusów, stereometria. Zaraz zerknę zadanko

13 sty 21:17
Saizou :
Dlatego trzeba ćwiczyć swoje słabsze strony, żeby potem było łatwiej.
Lepiej, żeby teraz się klika razy naciąć niż na maturze.
W zadaniu wystarczy wykorzystać podstawy geometrii

13 sty 21:20
salamandra:
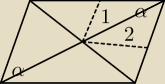
α= 60
Dobry rysunek wstępny? Dobrze zrozumiałem polecenie?
13 sty 21:21
Saizou : tylko te odcinki 1 i 2 pod kątem prostym
13 sty 21:21
salamandra: Wiem, tylko nie wiedziałem jak je oznaczyć w tym magicznym rysowaniu

13 sty 21:22
salamandra: Opłaca się wykorzystać jakoś kąt między tymi odcinkami? będzie tam 120 stopni
13 sty 21:26
Saizou : To zależy jaką drogą pójdziesz. Ja mam rozwiązanie na 4 linijki

13 sty 21:28
salamandra: Dużo pomogłoby mi info, czy te przekątne dzielą kąt α na pół, wątpię, ale spytam
13 sty 21:29
Saizou :

13 sty 21:30
salamandra: Zaraz spróbuje, mam pomysł
13 sty 21:52
salamandra:
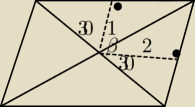
β= 120 stopni
Do tego momentu jest ok?
13 sty 22:06
salamandra:
Jeśli tak to
13 sty 22:15
Saizou :
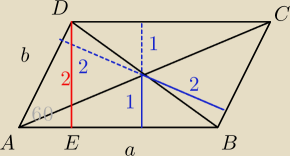
Pole na dwa sposoby
2a=4b ⇒ a=2b
| | √3 | | 2 | | 4√3 | | 8√3 | |
sin60= |
| = |
| →b= |
| a= |
| |
| | 2 | | b | | 3 | | 3 | |
z tw. cosinusów
|BD|
2= b
2+a
2−2ab*cos60 →|BD|=U{
√4√3{3}
|AC|
2=b
2+a
2+2ab*cos60 → |AC|=4
13 sty 22:32
13 sty 22:33
salamandra: Chociaż kawałek dobrze

Twierdzenia cosinusów nie miałem. Dałoby radę z mojego sposobu wyznaczyć f? Jakoś nie moge się
dopatrzec, „e” łatwo poszło
13 sty 22:37
Saizou : kąt β u ciebie ma 60 stopni
13 sty 22:38
a@b:
W każdym równoległoboku zachodzi taka równość
f2+e2=2a2+2b2
13 sty 22:40
salamandra: A czemu nie 120?
13 sty 22:42
Saizou :
Eta nie każdy zna tę zależność, ja na przykład nie powiedziałbym jej z pamięci.
bez tw. cosinusów
|AE| da się obliczyć z tw Pitagorasa
|EB| poprzez odejmowanie
|DB| Pitagoras
Druga przekątna
"Przeklejamy" ΔAED tak aby boki AD i BC się pokryły (i znowu Pitagoras )
13 sty 22:43
Saizou :
Przeprasza, dobrze, źle spojrzałem u siebie na rysunek
13 sty 22:44
a@b:
No to mamy nowe zadanko( typu "wykaż"
zad
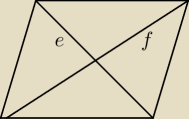
Wykaż ,że w każdym równoległoboku zachodzi równość
f
2+e
2=2a
2+2b
2
gdzie a,b, −− dł. boków i f,e −−− dł. przekątnych

13 sty 22:46
Saizou :
2 x tw. cosinusów
13 sty 22:48
salamandra: Ogarnę jutro ten sposób z 22:43.
Czyli da radę z tego mojego rysunku wykombinować tę druga przekątną? I jeszcze pytanie do
Twojego rysunku− skąd wynika, że ta „czerwona” wysokość = 2? Czyli ta odległość od punktu
przecięcia do boku to 1/2h?
13 sty 22:48
Saizou :
| | 1 | |
Tak, odległość punktu przecięcia do boku wynosi |
| h, stąd też czerwony odcinek ma długość |
| | 2 | |
2
13 sty 22:51
a@b:
Dokładnie tak
Saizou
Dlatego w rombie mamy równość
f2+e2=4a2

13 sty 22:52
Saizou :
Tam nie masz po 30o.
13 sty 22:54
a@b:
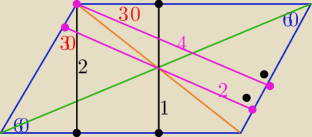
@
salamandra
A może taki rys. Ci pomoże?
13 sty 22:56
salamandra: To czemu wyszło?

13 sty 22:57
Saizou : Przypadek
13 sty 23:01
salamandra: To skoro tam nie jest 30, to jedyne co bym potrafił to obliczyć a i b,
Te dwa podpunkty co napisałeś, że bez tw. cosinusów tez, nie wiem natomiast jak DB z Pitagorasa
13 sty 23:03
Saizou :
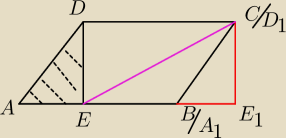
Tak ja w podstawówce wyprowadzało się wzór na pole

13 sty 23:05
Saizou :
Zadanie 2 czeka na rozwiązanie Maturzyści
W trapezie o kątach ostrych 30° i 60°, zaś różnica kwadratów przekątnych trapezu wynosi 16
Oblicz pole tego trapezu.
14 sty 14:11
salamandra:
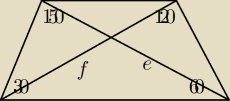
e
2−f
2 = 16
(e−f)(e+f) = 16
Jakaś wskazówka?
14 sty 20:53
Saizou :
skorzystać z trójkątów 30, 60, 90
14 sty 20:54
salamandra: W sumie to odwrót, bo nie mogę założyć która przekątna jest dłuższa, bo gdyby się okazało, że f
jest dłuższe, to wyszedłby mi ujemny wynik
14 sty 20:54
salamandra: Przekątne w trapezie również tworzą dwusieczne?
14 sty 20:56
Saizou :
Przekątne to nie dwusieczne.
Ta przekątna naprzeciwko 60° będzie dłuższa.
14 sty 20:59
salamandra:

Jedyne co mi przychodzi do głowy to jakieś wysokości dorysować, np. tak?
14 sty 21:03
a@b:
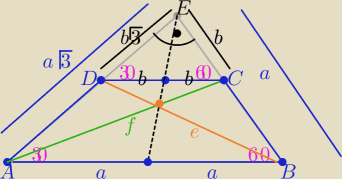
Z trójkątów o kątach : 30
o,60
o,90
o ( wprowadzamy oznaczenia jak na rys.
| | √3 | |
P (trapezu)= P(ABC)−P(DEC) ( a2−b2)* |
| |
| | 2 | |
w ΔAEC : f
2=3a
2+b
2
w ΔBDE : e
2=a
2+3b
2
− ============
f
2−e
2=2(a
2−b
2) ⇒ a
2−b
2=8
P=4
√3
========
14 sty 21:40
Saizou :
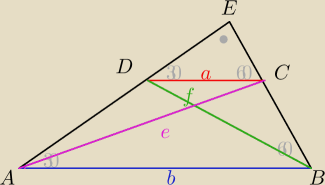
Podpowiedź:
opisz długości odcinków, które wynikają z własności trójkątów 30, 60, 90
założenie e>f
14 sty 21:40
a@b:
Sorry
Saizou za zepsucie zabawek

14 sty 21:41
Saizou :
Eta nic się nie stało

możesz coś wrzucić dla naszych rodzynków?
14 sty 21:42
Saizou :
Zadanie (nie wiem które, ale niech będzie) 4*
Dany jest trapez prostokąty ABCD o podstawach AB i CD, dłuższym ramieniu o długości 8√3
oraz kącie ostrym równym 30°, Oblicz pola trójkątów AOB oraz DOC, gdzie O jest punktem
przecięcia przekątnych trapezu, jeżeli jego obwód jest równy 12√3+24.
14 sty 21:45
salamandra: | | √3 | |
P (trapezu)= P(ABC)−P(DEC) (a2−b2)* |
| skąd to wynika? resztę rozumiem |
| | 2 | |
14 sty 21:47
Saizou : Tam powinno być dodać
P
trapezu=P
ABC+P
DCE
| | 1 | | 1 | | 1 | |
PACD=P{ACE}−PDEC= |
| •a√3•b− |
| •b√3•b= |
| b√3(a−b) |
| | 2 | | 2 | | 2 | |
analogicznie
P
ABC=P
ABE−
ACE
14 sty 21:54
Saizou :
Poprawka
P=PACD+PABC
14 sty 21:55
mr t: Ciekawe zadanka saizou, miło z twojej strony ze się angażujesz

17 lut 18:42
salamandra: Miesiąc minął, a ja nie pamiętam swoich postów z tego wątku

17 lut 18:55
17 lut 19:02
salamandra: Spróbuję później je rozwiązać ponownie− może się uratuje

17 lut 19:34
mr t:
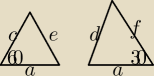

Może ktoś wie jak rozwiązać zadanie 2, obliczyć pole trapezu o katach ostrych 30 i 60 i różnicy
kwadratów przekątnych równej 16?
Rozrysowalem sobie dwa trójkąty, z tw cosinusów rozpisałem dwa równania które później odjalem:
e
2−d
2=c
2−f
2−ac−
√3af → 16=c
2−f
2−ac+
√3af
17 lut 19:49
mr t:
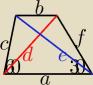
tutaj rysunek z opisanymi bokami:
17 lut 19:52
a@b:
Odp: P=4√3
======
17 lut 20:03
a@b:
Czytaj mój wpis (Eta 21:40
Czego tu nie rozumiesz ?
17 lut 20:06
mr t: Kurcze, głupio się przyznac nie szukałem aż tak nisko, dzięki − wszystko jasne

17 lut 20:14
a@b:

17 lut 20:17
a@b:
No i jeszcze
100 wpis mój

17 lut 20:19


 Odp: L=7,2√5
=========
Odp: L=7,2√5
=========




 Odnośnie pierwszego.
Wybaczcie za rysunek, ale tylko mam pytanie, czy tam gdzie "x" będzie kąt prosty?
Odnośnie pierwszego.
Wybaczcie za rysunek, ale tylko mam pytanie, czy tam gdzie "x" będzie kąt prosty?

 Ile wynosi suma miar kątów przy jednym ramieniu trapezu?
Ile wynosi suma miar kątów przy jednym ramieniu trapezu?
 Ok, spróbuje tu:
2α+45+45 = 180
2α = 90
α = 45
więc kąt "x" to dopełnienie do 180, i jest prosty.
Ok, spróbuje tu:
2α+45+45 = 180
2α = 90
α = 45
więc kąt "x" to dopełnienie do 180, i jest prosty.
 Równość pól
Równość pól

 BC z Pitagorasa
BC z Pitagorasa
 Obwód : 4r+2(x+y)
W ΔBCS : x+y=√22+42= 2√5
Obwód : 4r+2(x+y)
W ΔBCS : x+y=√22+42= 2√5




 Jak będziesz ćwiczyć to dasz radę.
Jak będziesz ćwiczyć to dasz radę.


 α= 60
Dobry rysunek wstępny? Dobrze zrozumiałem polecenie?
α= 60
Dobry rysunek wstępny? Dobrze zrozumiałem polecenie?



 β= 120 stopni
Do tego momentu jest ok?
β= 120 stopni
Do tego momentu jest ok?
 Jeśli tak to
Jeśli tak to
 Pole na dwa sposoby
2a=4b ⇒ a=2b
Pole na dwa sposoby
2a=4b ⇒ a=2b
 Twierdzenia cosinusów nie miałem. Dałoby radę z mojego sposobu wyznaczyć f? Jakoś nie moge się
dopatrzec, „e” łatwo poszło
Twierdzenia cosinusów nie miałem. Dałoby radę z mojego sposobu wyznaczyć f? Jakoś nie moge się
dopatrzec, „e” łatwo poszło


 @ salamandra
A może taki rys. Ci pomoże?
@ salamandra
A może taki rys. Ci pomoże?

 Tak ja w podstawówce wyprowadzało się wzór na pole
Tak ja w podstawówce wyprowadzało się wzór na pole 
 e2−f2 = 16
(e−f)(e+f) = 16
Jakaś wskazówka?
e2−f2 = 16
(e−f)(e+f) = 16
Jakaś wskazówka?
 Jedyne co mi przychodzi do głowy to jakieś wysokości dorysować, np. tak?
Jedyne co mi przychodzi do głowy to jakieś wysokości dorysować, np. tak?
 Z trójkątów o kątach : 30o,60o,90o ( wprowadzamy oznaczenia jak na rys.
Z trójkątów o kątach : 30o,60o,90o ( wprowadzamy oznaczenia jak na rys.
 Podpowiedź:
opisz długości odcinków, które wynikają z własności trójkątów 30, 60, 90
założenie e>f
Podpowiedź:
opisz długości odcinków, które wynikają z własności trójkątów 30, 60, 90
założenie e>f

 możesz coś wrzucić dla naszych rodzynków?
możesz coś wrzucić dla naszych rodzynków?






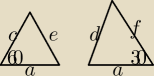
 Może ktoś wie jak rozwiązać zadanie 2, obliczyć pole trapezu o katach ostrych 30 i 60 i różnicy
kwadratów przekątnych równej 16?
Rozrysowalem sobie dwa trójkąty, z tw cosinusów rozpisałem dwa równania które później odjalem:
e2−d2=c2−f2−ac−√3af → 16=c2−f2−ac+√3af
Może ktoś wie jak rozwiązać zadanie 2, obliczyć pole trapezu o katach ostrych 30 i 60 i różnicy
kwadratów przekątnych równej 16?
Rozrysowalem sobie dwa trójkąty, z tw cosinusów rozpisałem dwa równania które później odjalem:
e2−d2=c2−f2−ac−√3af → 16=c2−f2−ac+√3af
 tutaj rysunek z opisanymi bokami:
tutaj rysunek z opisanymi bokami:


