PLISSSS jak najszybciej, nie wiem jak zrobić :( ZombieAZA: Na paraboli y=x² wyznacz punkt A tak, aby pole trójkąta ABC, gdzie B i C to punkty przecięcia paraboli z prostą y=x+2, było największe.

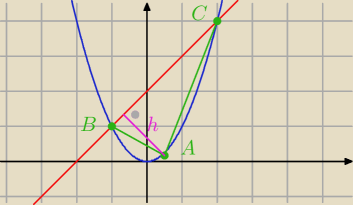
Saizou : A=(x, y)=(x, x²) B = (−1,1) C = (2, 4) |BC|=.... = podstawa trójkąta h − odległość punkty A od prostej BC (wysokość trójkąta) Dalej sam/sama

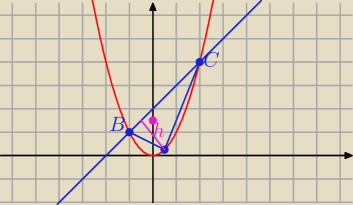
janek191: B = ( − 1. 1) C = ( 2, 4) A = ( x, x² Prosta BC : x − y + 2 = 0 h − odległość punktu A od prostej BC Mamy

	I 1*x − 1*x2 + 2 I		I x − x2 + 2I
h =		=
	√ 1 + 1		√2

I BC I = 3√2 Pole Δ ABC

	I − x2 + x + 2I
P = 0,5*I BC I * h = 0,5* I 3√2*		=3 I − x2 + x + 2 I
	√2

	1
P jest największe dla x =
	2

	1		1
A = (		,		)
	2		4

4214123: <script>alert("matematyka jest cool!")</script>

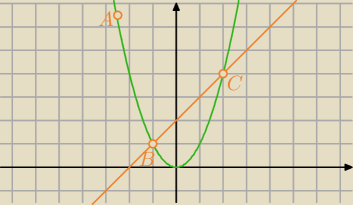
Tadeusz: ... coś chyba brakuje w treści Przecież np to będzie wieksze

janek191: W ten sposób można otrzymać Δ o dowolnym polu Faktycznie coś brakuje

Jerzy: Pewnie dziedzina zawężona do <−1,2>

ZombieAZA: Jak czegoś brakuje? Taka miałam treść

ZombieAZA: A może w treści było pole najmniejsze a nauczyciel zmienił na największe?

ZombieAZA: W takim przypadku jak miało by to wyglądać?

Jerzy: 14:58

ZombieAZA: Hmm okeej, dzięki wielkie

janek191: Tam pole powinno być równe P = 1,5 I − x² + x + 2 I ale to nie zmienia wyniku rozwiązania.

Tadeusz: ... zadanie z "pole najmniejsze" w tym przypadku nie miałoby żadnego sensu

ZombieAZA: Dlaczego?

Tadeusz: bo mówiąc po chłopsku "takie pole dąży do 0"

ZombieAZA: Aaa okej, dziwię się bardzo więc dlaczego ktoś układa takie zadania

Tadeusz: może w treści zadania było że A leży poniżej danej prostej lub na paraboli pomiędzy B i C

ZombieAZA: Nic więcej nie ma, słowo w słowo przepisane więc nie moja wina

Tadeusz: ... moja też nie

janek191: I rok studiów, czy szkoła średnia?

ZombieAZA: Liceum ale matma rozszerzona

ZombieAZA: No nic, nic więcej nie da się wykombinować. Dzięki wielkie wszystkim za pomoc

janek191:

janek191: Podobne zadanie było 11 stycznia o 12.59 ( jest u mnie ). 395539

ZombieAZA: Takie pytanie jeszcze do janek191 ta długość odcinka BC to skąd 3 pierwiastki z 2? Mi wyszło pod pierwiastkiem 9 + 4 to pierwiastek z 13

ZombieAZA: Ok już widzę mój błąd

Tadeusz: √9+9=3√2

ZombieAZA: Ale nadal nie rozumiem skąd wniosek po obliczeniu pola,ze jest ono największa dla 1/2

jc: To ogólny takt: należy przeciąć pionową linią środek odcinka AB. Pionowa prosta przetnie w parabolę w szukanym puncie C.

janek191: Funkcja f(x) = − x² + x + 2

	− b		−1		1
przyjmuje największą wartość dla x =		=		=		, bo a = − 1 < 0
	2a		−2		2

jc: Uzasadnienie. Największe pole będzie miał najwyższy trójkąt. Wierzchołek takiego trójkąta leży w miejscu w którym styczna jest równoległa do AB. Punkt styczności leży w punkcie opisanym powyżej. Można też inaczej: A=(a,a²), B=(b,b²), C=(c,c²).

	1		1		1
Pole =		(b−a)(b−c)(c−a) =		(b−a)[ (b−a)2 − (2c−a−b)2 ] ≤		(b−a)3
	2		8		8

Równość mamy dla c=(a+b)/2.