aksjomat Wolfik:

	a+b
Niech a<b<c oraz f(x)=(x−a)(x−b)(x−c). Uzasadnij, że f(		)>0
	2

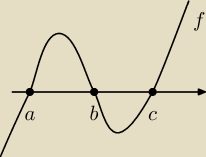
Saizou : Zadajmy dla jakich x funkcja f przyjmuje wartości dodatnie. x∊(a,b) ∪ (c, +∞)

	a+b
Wystarczy pokazać, że w tym przedziale mieści się x=
	2

Wolfik:

	b−a		a−b		a+b−2c
f(		)(		)(		)
	2		2		2

b−a jest >0 a−b<0 ⇒iloczyn jest dodatni i >0 a+b−2c<0 CND dobrze?:(

Saizou : W zadaniu masz powiedziane tylko, że a<b<c nie wiadomo czy są to liczby większe od zera

jc: Co to jest? CND? Chyba jednak coś innego.

Wolfik:

	a+b
skoro (a,b)>0 to a+b>0 i		>0?
	2

CND(co należało dowieść)

jc: Należało dowieść, że a+b−2c < 0?

Wolfik:

	a+b
należało dowieść, że f(		)>0 nie wiem co mam dalej zrobić
	2

Saizou : Przedział nie może być > 0 idąc twoim tokiem rozumowania

	a+b		b−a		a−b		a+b−2c
f(		)=		•		•
	2		2		2		2

	b−a
Z założenia mamy, że a<b → b−a > 0 →		> 0
	2

	a−b
Z założenia mamy, że a<b → a−b < 0 →		< 0
	2

Należy pokazać, że a+b−2c<0 a<c b<c ====+ a+b<2c a+b−2c<0

Wolfik: a+b<2c⇒a+b−2c<0 tylko co jeśli a,b,c są <0? i tak one zamienią się na dodatnie przez to, że np. a<b?

Saizou : Tak, zauważ, że nie uwzględnialiśmy znaków poszczególnych liczb, jedynie wyrażeń.

Wolfik: ale w tym przypadku wystarczą same wyrażenia i to jest już skończony dowód?

Saizou : + komentarz o iloczynie 3 liczb z czego jedna jest dodatnia, a dwie ujemne, zatem iloczyn jest dodatni

Wolfik: dziękuję bardzo!