Cosinus kąta między ścianami bocznymi w ostrosłupie
Mirek: Cześć, mam problem z tym zadaniem:
W ostrosłupie czworokątnym ABCDS podstawa ABCD jest kwadratem, a wysokość AS
jest 4 razy dłuższa od krawędzi podstawy. Oblicz cosinus kąta między ścianami BCS i CDS
tego ostrosłupa.
Wydaje mi się, że trzeba policzyć pole BCS (albo CDS), mając wysokość wychodzącą z wierzchołka
ostrosłupa i krawędź podstawy, a następnie przyrównać do |SC|*hB/2 (albo hD) i obliczyć hB
(albo hD). Następnie w trójkącie równoramiennym, w którym
ramiona mają długość hB i podstawa tr. jest przekątną podstawy ostrosłupa, użyć tw. cosinusów.
Nie wiem tylko, jak obliczyć tę wysokość wychodzącą z wierzchołka (lub ogólnie pole BCS albo
CDS)
13 sty 12:17
Saizou :
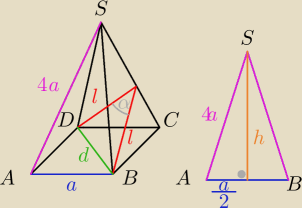
Zakładając, że jest ro ostrosłup prawidłowy czworokątny, to mamy
1/ z tw. Pitagorasa h
2/ l z równości pól
3/ d przekątna kwadratu
4/ tw. cosinusów
13 sty 12:35
Saizou :
Lepiej przyjąć że długość podstawy to 2a niż a. Nie będzie wtedy ułamków
13 sty 12:36
Mirek: Dzięki, tylko mam pytanie czy skoro krawędź AS jest jednocześnie wysokością, to możemy
w ogóle założyć, że ten ostrosłup jest prawidłowy?
13 sty 12:56
Saizou : nie doczytałem

sorry, mój bład
Za chwilę napiszę poprawkę
13 sty 12:58
Saizou :
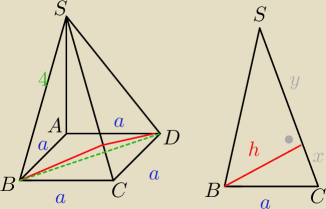
SD = SB z Pitagorasa
SC z Pitagorasa (wys. i przekątna podstawy)
h (2x Pitagoras + x+y=SC → układ równań)
13 sty 13:12
Mirek: Dzięki wielkie
13 sty 13:15
 Zakładając, że jest ro ostrosłup prawidłowy czworokątny, to mamy
1/ z tw. Pitagorasa h
2/ l z równości pól
3/ d przekątna kwadratu
4/ tw. cosinusów
Zakładając, że jest ro ostrosłup prawidłowy czworokątny, to mamy
1/ z tw. Pitagorasa h
2/ l z równości pól
3/ d przekątna kwadratu
4/ tw. cosinusów
 sorry, mój bład
Za chwilę napiszę poprawkę
sorry, mój bład
Za chwilę napiszę poprawkę
 SD = SB z Pitagorasa
SC z Pitagorasa (wys. i przekątna podstawy)
h (2x Pitagoras + x+y=SC → układ równań)
SD = SB z Pitagorasa
SC z Pitagorasa (wys. i przekątna podstawy)
h (2x Pitagoras + x+y=SC → układ równań)