W równoległoboku ABCD bok DC ma długość dwukrotnie większą n: W równoległoboku ABCD bok DC ma długość dwukrotnie większą od długości promienia okręgu r opisanego na trójkącie ABD (rysunek w linku, niestety nie jestem sobie w stanie poradzić z rysowaniem tutaj ). Wiedząc, że kąt ostry tego równoległoboku ma miarę 30°, wykaż, że stosunek długości sąsiednich boków równoległoboku ABCD jest równy √3/2 . https://imgur.com/TtQHOsI

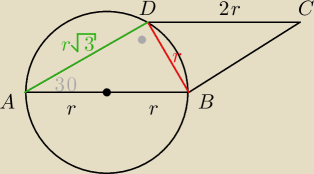Saizou : ΔABD jest prostokątny (30, 60, 90), ponieważ kąt ADB jest oparty na średnicy. |AB|=2r, ponieważ |AB|=|CD| (z własności równoległoboku) Wówczas mamy |BD|=r |AD|=r√3, zatem

|AD|		r√3		√3
	=		=
|BD|		2r		2