Pochodna M: Wiecie może od czegp tu zacząć? napisz rownania stycznych do wykresu funkcji f(x) = x² przecinających osie układu współrzędnych xOy w takich punktach A i B, aby AOB miał pole 2.

Blee: 1) wzór na styczną do funkcji f(x) w punkcie C(x₀,y₀) y = f'(x₀)*(x−x₀) + f(x₀) ⇔ y = 2x₀(x−x₀) + x₀² ⇔ y = x₀(2x − 2x_o + x_o) ⇔ ⇔ y = x₀(2x − x₀) 2) punkty przecięcia się z osiami: a) z osią OX

	x0
0 = x0(2x−x0) −> (dla x0 ≠ 0 mamy wtedy) x =
	2

b) z osią OY y = −x₀² 3) zauważ, że otrzymujesz trójkąt prostokątny o przyprostokątnych długości:

	x0
|		| oraz |−x02|
	2

	x0		x03
PΔ = |		|*|−x02| = |		| = 2 ⇔ x0 = ±3√4
	2		2

4) wracamy do do wzoru stycznej i podstawiamy te x₀ 5) SPRAWDZAMY

Blee: tfu ... zapomniałem podzielić przez 2 w polu ... więc x₀ = ± 2 (o wiele ładniejsza liczba )

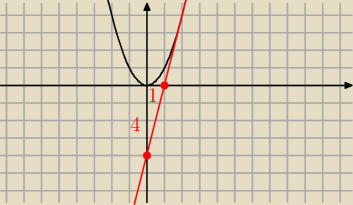
Blee: na rysunku zaprezentowana JEDNA z dwóch stycznych spełniających ten warunek ... zauważ, że faktycznie − masz trójkąt o przyprostokątnych równych 1 i 4 ... więc pole tego trójkąta to faktycznie 2[j²]

M: Dzieluję bardzo za wytłumaczenie sama bym na to nie wpadla