Dla maturzystów
Saizou : Zad 1
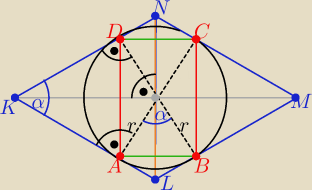
Na okręgu i promieniu r opisano romb, a punkty styczności są wierzchołkami czworokąta ABCD.
Oblicz długość boku a rombu i długości d
1 i d
2 przekątnych rombu,
| | 8 | |
wiedząc, że stosunek pole P1 rombu do pola P2 czworokąta ABCD jest równy |
| |
| | 3 | |
12 sty 22:00
a@b:
| | 1 | |
P(rombu) =P1=a2sinα i P(ABCD)=P2= |
| *|AC|*|BC|= 2r2 |
| | 2 | |
| P1 | | 8 | | 2r2 | | 3 | | r | | √3 | | 4r√3 | |
| = |
| ⇒ |
| = |
| ⇒ |
| = |
| ⇒ a= |
| |
| P2 | | 3 | | a2 | | 8 | | a | | 4 | | 3 | |
| | 2r | | √3 | |
h=2r i sinα= |
| = |
| ⇒kąt ostry α=60o |
| | a | | 2 | |
zatem romb składa się z dwu trójkątów równobocznych o boku "a"
| | 4r√3 | |
a= |
| = d1=|NL| to d2=|KM|=a√3 =4r |
| | 3 | |
=================================
12 sty 23:21
Saizou : @[F[Eta yy dla maturzystów, ale na zdrowie
12 sty 23:28
ABC:
egzaminator też musi ćwiczyć
12 sty 23:30
a@b:
Sorry
Nie ma maturzystów ... więc sobie ot tak....
12 sty 23:46
a@b:
| | 1 | |
Poprawiam zapis ... P(ABCD)=P2= |
| *|AC|*|BD|*sinα |
| | 2 | |
12 sty 23:49