aksjomat
Wolfik: Rozwiąż nierówność:
| 6x | | 12x | | 12x | |
| −√ |
| −24√ |
| >0 |
| x−2 | | x−2 | | x−2 | |
12 sty 13:48
Des:
+ odpowiednie założenia
12 sty 14:06
Wolfik: zał: x≠2 i x≠0
t4−2t2−4t>0
teraz znowu podstawienie, czy lepiej będzie ze schematu hornera?
12 sty 14:15
Saizou :
Założenie jest inne
12x(x−2)≥0 i x≠2
x∊(−
∞;0> ∪ (2;+
∞)
t
4−2t
2−4t>0
t(t
3−2t−4)>0
i rozkład wielomianu, wężyk i powrót z podstawieniem i uwzględnienie założeń
12 sty 14:23
Wolfik: t(t−2)(t2+2t+2)>0
t=0 v t=2 v Δ=4−4*2<0
będzie tutaj wężyk? : /
12 sty 14:37
Des: Rozłóż jeszcze 3 nawias
12 sty 14:40
Des: A jednak nie
12 sty 14:40
salamandra:
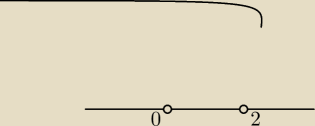
12 sty 14:44
Des: Wężyk będzie, pomijasz tylko 3 nawias bo tam nie ma miejsc zerowych ale uwzględniasz
współczynnik przy najwyższej potędze
(Ja nie potrafię tu rysować :< )
12 sty 14:44
Des: Nie tylko ja

12 sty 14:45
salamandra:
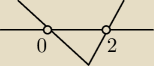
coś źle mi działa to rysowanie, wyżej chciałem niby "wężykiem"
12 sty 14:45
Wolfik: a, czyli chodzi o wężyk funkcji kwadratowej? jeśli tak to wyszło mi, że t∊(0,2)
12 sty 14:50
Des: Właśnie o to chodzi, ale t∊( −∞ , 0 )∪(2 , ∞)
12 sty 14:55
Wolfik: kolejna głupota moja... co mi teraz da podstawienie pod t tego pierwiastka 4 stopnia?
12 sty 14:58
Des: Jeszcze trzeba zrobić konfrontację tego przedziału z początkowym założeniem, t>0
12 sty 15:00
Des: Czyli t>2
12 sty 15:00
12 sty 15:04
12 sty 15:04
Jerzy:
A dlaczego t nie może równać się 0 ?
12 sty 15:07
Wolfik: 12x(x−2)<16(x−2)
12x>16(x−2)
x<8
12 sty 15:07
Wolfik: skoro z nierówności wyszedł przedział od (−∞,0)U(2,+∞) to nie skreśla nam warunku początkowego
t≥0?
w takim razie powinno być t∊{0}U(2,+∞)?
12 sty 15:20
Des: 0 odpada
Dla t=0
04 − 2*02 −4* 0 > 0
0>0
12 sty 15:26
Jerzy:
t ∊ <2,∞)
12 sty 15:28
Jerzy:
@Des,14:06, dlaczego pierwiastek nie może być równy 0 ?
12 sty 15:30
Des: Wolfik, podnosząc do potęgi 4 dostaniesz moduł po lewej
12 sty 15:32
Wolfik: czemu <2,
∞), a nie (2,
∞), jesli z nierownosci wyszedl przedzial od 2 otwarty?

12 sty 15:32
Des: Może być, pewnie chodzi Ci o wpis z 15:00, tam powinno być ≥ zamiast >
12 sty 15:34
Des: Ale biorąc cześć wspólną 0 i tak odpada
12 sty 15:35
Wolfik: nie wiem czy wiem o co chodzi
| | 12x | |
z początkowego założenia dostajemy, że |
| ≥0 i x≠0, czyli jest x∊(−∞,0>U(2,∞) |
| | x−2 | |
| | 12x | |
następnie pod t podstawiliśmy 4√ |
| ] i t≥0 bo wyrażenie pod pierwiastkiem może być |
| | x−2 | |
większe lub równe 0
później nierówność: t(t−2)(t
2+2t+2)>0, z tego wychodzi t=0 v t=2 i rysujemy wężyk z którego
wychodzi t∊(−
∞,0)U(2,+
∞), ale w założeniu jest t≥0 więc zostaje t∊(2,+
∞)
dlaczego t∊<2,
∞), a nie t∊(2,
∞) skoro tak wychodzi z nierówności?
| | 12x | |
później rozwiązuje nierówność 4√ |
| ]>2, z której wychodzi mi x<8... |
| | x−2 | |
12 sty 15:47
Des: t∊ (2, ∞)
15:07, zjadłeś jeden nawias po prawej stronie
12x(x−2) > 2(x−2)2
12 sty 15:57
Wolfik: 12(x−2)>16(x−2)
2
3>4x−8
4x<11
x<11/4
12 sty 16:04
Des: Do kwadratu zapominasz podnieść
12 sty 16:05
Wolfik: nie mogę skrócić (x−2) po lewej z (x−2)2, żeby po prawej zostało samo (x−2)?
12 sty 16:07
Des: Specjalnie podnosimy do kwadratu mianownik, bo nie wiadomo jakiego jest znaku (wtedy mamy
pewność, że jest >0)
12 sty 16:08
ABC:
przy takim skracaniu w nierówności musisz przypadki rozpatrywać w zależności od znaku x−2
12 sty 16:09
Des: A dzieląc przez (x−2) nie wiesz czy dzielisz przez coś dodatniego czy ujemnego..
12 sty 16:10
Wolfik: 12(x−2)>16(x−2)
2
12x−24>16(x
2−4x+4)
12x−24>16x
2−64x+64
0>166x
2−76x+88
pierwiastek z delty=12
x
1=2 nie nalezy do dziedziny
x
2=27,5?

12 sty 16:20
Wolfik: skoro chce się pozbyć pierwiastka 4 stopnia to podnoszę obustronnie do potęgi 4
| | 12 | |
więc z lewej |
| , a z prawej nie powinienem mieć 16? |
| | x−2 | |
dlaczego jest 12x(x−2)>2(x−2)
2? ................
12 sty 16:22
Des:
12x2 − 24x > 16(x2 −4x + 4)
12x2 − 24x > 16x2 − 64x + 64
4x2 − 40x + 64 < 0
x2 − 10x + 16 < 0
12 sty 16:24
Wolfik: zgubiłem iksa na początku, dlatego mi nie wychodziło
12 sty 16:25
Wolfik: x∊(2,8)
dziękuję za pomoc :'))
12 sty 16:29


 coś źle mi działa to rysowanie, wyżej chciałem niby "wężykiem"
coś źle mi działa to rysowanie, wyżej chciałem niby "wężykiem"

