Cosinus kąta rozwarcia stożka Paweł: Cześć, mam problem z tym zadaniem: W stożek o promieniu podstawy długości 4 wpisano kulę o promieniu 2. Wyznacz cosinus kąta rozwarcia stożka.

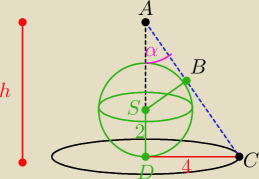
xyz: kat ktorego szukamy to 2*α Oznaczmy wierzcholki te po prawej jako A,C oraz punkt stycznosci do ramienia jako B wtedy trojkaty ABS i BCS sa podobne (kkk) odcinek |BC| wynosi 4 bo idac z dowolnego punktu do punktow stycznosci okregu to odleglosci od tego punktu do tych punktow stycznosci sa takie same. zatem mozemy ulozyc proporcje

|AB|		|AD|
	=
|BS|		|DC|

niech |AD| = h (wysokosc tego trojkata) niech |AB| = x |BS| = 2, |DC| = 4

x		h
	=		−−> h = 2*x
2		4

i teraz z pitagorasa w trojkacie ADC |AD|² + |DC|² = |AC|² h² + 4² = (4+x)² (2*x)² + 4² = (4+x)² 4x² + 16 = 16 + 8x + x² 3x² − 8x = 0 x(3x−8) = 0

	8
x = 0 ∉ D lub 3x−8 = 0 −−−> x =
	3

	8		20
w takim razie |AC| = 4+x = 4 +		=
	3		3

czyli

	4		12		3
sin α =		=		=
	20   3		20		5

α ≈ 37^o zatem kat rozwarcia stozka = 2*α = 74^o

xyz: poprawka trojkaty ABS i ADC sa podobne (kkk)

Paweł: Dzięki bardzo

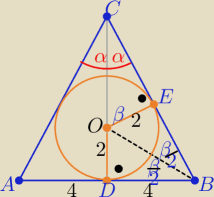a@b: W zadaniu mamy podać dokładną wartość cos2α ( a nie przybliżoną miarę kąta) ====================================== Proponuję tak : ( jeden ze sposobów) W ΔDOB : |OB|=2√5 to sin (β/2)=1/√5 i cos(β/2)=2/√5 w ΔOEC : sinβ= cosα to cosα=2sin(β/2)*cos(β/2) ⇒ cosα=4/5 zatem cosinus kąta rozwarcia stożka: cos(2α)= 2cos²α−1 = .........

	7
cos(2α)=
	25

============= i po ptokach

xyz: sin α = 3/5 cos(2α) = cos²α−sin²α = 1 − 2sin²α = 1 − 2 * (3/5)² = 1−18/25 = 7/25

a@b: