aksjomat Wolfik: Wyznacz te wartości m dla których suma odwrotności pierwiastków równania:

mx		m+2
	+		=x+2√2
m−2		x

	√2
jest mniejsza od
	m−1

Pierwszą część zadania zrobiłem, czyli:

x1+x2		2√2(m−2)		2√2
	=		=
x1x2		(m2−4)		m+2

teraz mam problem z rozwiązaniem tego: zał: m≠1 i m≠−2 i m≠2

2√2		√2
	<		/*(m+2)2(m−1)2
m+2		m−1

2√2(m+2)(m−1)²<√2(m−1)(m+2)² 2(m−1)<m+2 2m−2<m+2 m<4 gdzie mam błąd?

a@b: Jakie masz równanie kwadratowe po przekształceniu ... napisz, to sprawdzę

Wolfik: w którym miejscu dokładnie?

Wolfik: jeśli chodzi o to jeszcze z początku zadania to: 2x²−(2√2m−4√2)x+m²−4=0

a@b: x≠0 i m≠ 2 przekształcam równanie do równania kwadratowego z niewiadomą x mx²+(m²−4)= x²(m−2) +2√2(m−2)x 2x²−2√2(m−2)x+m²−4=0 ====================== teraz : Δ.... i wzory Viete^'a i założenie m≠2

Wolfik: jaka jest różnica między: −2√2(m−2), a −(2√2m−4√2)?

a@b: Nie ma żadnej Nie napisałeś wcześniej tego równania , dlatego pytałam jakie jest to równanie Duchem nie jestem....

Wolfik: delta musi być większa od zera, żeby były 2 pierwiastki z delty mam przedział m∊(−∞,2)

	2√2(m−2)		2√2
z wzorów Viete'a mam to co wcześniej, czyli		=
	m2−4		m+2

Wolfik: i po tym właśnie nie wychodzi mi rozwiązanie tej nierówności

a@b: Mnie wyszła Odp: m∊(−∞, −2)

a@b: z delty : m∊( −∞, 0) U (2,∞) i z podanego warunku: m∊(−∞, −2)

Wolfik: Δ=(2√2m−4√2)²−8(m²−4)=8m²−32m+32−8m²+32=64−32m>0

a@b: Δ=8(m−2)²−8(m−2)(m+2) = 8(m−2)(m−2+m+2) = 16m(m−2)

a@b: Rzeczywiście u siebie widzę błąd 8(m−2)(m−2−m−2) = 64−32m czyli masz dobrze

a@b: zatem Δ>0 ⇒m∊(−∞,2) i z warunku m∊(−∞, −2) to odp: m∊(−∞, −2)

Wolfik: troche sie pogubilem mam delte m∊(−∞,2) o jaki warunek teraz chodzi z tym m∊(−∞,−2)?

Wolfik: po obliczeniu delty powinienem rozwiązywać już tę nierówność?

a@b:

	c		√2
2/ warunek widzę taki :		<
	a		m−1

	c		√2
a Ty napisałeś		<
	a		m+2

i ja go wzięłam nie patrząc wyżej na treść

	√2		√2
to w końcu jak ma być :		? czy		?
	m−1		m+2

Wolfik:

1		1		x1+x2		−b
	+		=		=
x1		x2		x1x2		a

−b		√2
	<
a		m−1

a@b:

x1+x2		−b   a		−b
	=		=
x1*x2		c   a		c

a@b: Taki ma być ten warunek! Poprzednio źle wpisałam ( nie założyłam okularów

a@b: Teraz działaj

wolfik: miałem na myśli c, a napisałem a : )) no i właśnie z tym warunkiem mam problem

wolfik: spróbuje jeszcze raz

wolfik:

	2√2		√2
w którym miejscu mam błąd od momentu:		<
	m+2		m−1

a@b: jaką masz odp w zbiorku

wolfik: m∊(−∞,−2)U(1,2)

a@b: po podzieleniu przez √2

2		1
	<
m+2		m−1

[(2m−2)−(m+2)](m+2)(m−1)<0 (m−4)(m+2)(m−1)<0 dokończ i będzie ok uwzględnij 1/ warunek z deltą

wolfik: to moje przeliczanie bez sensu było?

wolfik: i jakbyś mogła rozpisać to z 20.20 bo nie chce mi to wyjść : (

a@b: Dla wprawy Rozwiąż taką nierówność

3		1
	<
x+1		x+2

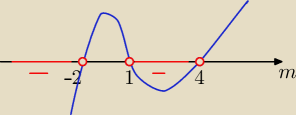
a@b: (2m−2−m−2)(m+2)(m−1)<0 ( m−4)(m+2)(m−1)<0

wolfik: zał: x≠−1 i x≠−2

3		1
	−		<0
x−1		x+2

3x+6−x−1
	<0/*(x+1)2(x+2)2
(x+1)(x+2)

(2x+5)(x+1)(x+2)<0 x=−5/2 v x=−1 v x=−2 x∊(−∞,−2,5)U(−2,−1)

a@b: ok

wolfik: baaaaaardzo dziękuję! dzisiaj już odpadam

a@b: Odpocznij trochę