Zadanie z plaszczyny Anastazja: Na płaszczyźnie OXY dana jest krzywa o równaniu y=1−x² dla −1<x<1 oraz punkty A(−1,−1), B(1,0). Na danej krzywej znaleźć taki punkt C, aby pole trójkąta ABC było największe.

Anastazja: Hej ludzie Proszę :'(

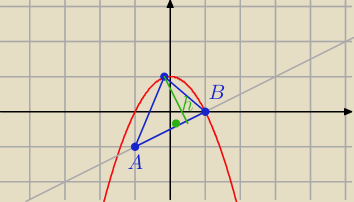
janek191: C = ( x, 1 − x²) pr AB: x − 2y − 1 = 0 Odległość C od prostej:

	I 1* x − 2*( 1 − x2) − 1I		I 2 x2 + x I
h =		=
	√1 + 4		√5

I AB I = √5 więc pole Δ ABC jest równe:

	I 2 x2 + x i
P = 0,5*√5*		= 0,5*I 2 x2 + x I = I x2 + 0,5 x I
	√5

P jest max dla x = − ¹₄

	1		15
C = ( −		,		)
	4		16

jak się nie pomyliłem