| h2 | ||
P= | ||
| tgα |
 ...moja ukochana planimetria
...moja ukochana planimetria 


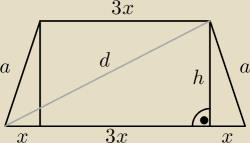 Zadanie 1
a − ramię trapezu
a=5√2
d − przekątna trapezu
d=√65
h − wysokość trapezu
b − górna podstawa
c − dolna podstawa
h2+9x2=d2 ∧ h2+x2=a2
h2=65−9x2 ∧ h2=50−x2
stąd:
65−9x2=50−x2
Zadanie 1
a − ramię trapezu
a=5√2
d − przekątna trapezu
d=√65
h − wysokość trapezu
b − górna podstawa
c − dolna podstawa
h2+9x2=d2 ∧ h2+x2=a2
h2=65−9x2 ∧ h2=50−x2
stąd:
65−9x2=50−x2
| 15 | √15 | √30 | ||||
15=8x2 ⇒ x2= | ⇒ x= | ⇒ x= | ||||
| 8 | 2√2 | 4 |
| 3√30 | ||
b=3x= | ||
| 4 |
| 5√30 | ||
a=5x= | ||
| 4 |
| 15 | ||
h2=50− | ||
| 8 |
| 385 | ||
h2= | ||
| 8 |
| √385 | √770 | |||
h= | ⇒ h= | |||
| 2√2 | 4 |
| 1 | ||
P= | *(a+b)*h | |
| 2 |
| 1 | 7√30 | √770 | 70√231 | 35√231 | ||||||
P= | * | * | = | = | ||||||
| 2 | 4 | 4 | 32 | 16 |
| 5√30 | √30 | |||
=4* | ||||
| 4 | 4 |
| 5√30 | ||
≠√30, zatem nie można w niego wpisać okręgu | ||
| 4 |
 rzeczywiście, (4x)2
rzeczywiście, (4x)2  wtedy x=1, górna podstawa 3, dolna 5, wysokość 7, pole 28 i nie można wpisać w niego okręgu,
bo 10√2≠8
wtedy x=1, górna podstawa 3, dolna 5, wysokość 7, pole 28 i nie można wpisać w niego okręgu,
bo 10√2≠8
 i rachunki przyjemniejsze
i rachunki przyjemniejsze
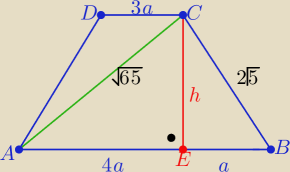 dwa razy z Pitagorasa
h2=65−16a2 i h2=50−a2
to 15a2=15 ⇒ a=1
|AB|=5 , |CD|=3 i h=7
dwa razy z Pitagorasa
h2=65−16a2 i h2=50−a2
to 15a2=15 ⇒ a=1
|AB|=5 , |CD|=3 i h=7
| a+b | ||
|AE|= | ||
| 2 |
| a+b | ||
P= | *h= 4a*h=28 | |
| 2 |
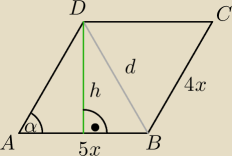 Zadanie 4
L − obwód rownoległoboku
L=18
L=18x
18x=18 ⇒ x=1
d − krótsza przekątna równoległoboku
liczymy pole ΔADB na dwa sposoby:
Zadanie 4
L − obwód rownoległoboku
L=18
L=18x
18x=18 ⇒ x=1
d − krótsza przekątna równoległoboku
liczymy pole ΔADB na dwa sposoby:
| 5h | ||
1) P= | ||
| 2 |
| 15 | 5 | 3 | 7 | 1575 | 15√7 | |||||||
2) P=√ | * | * | * | =√ | = | |||||||
| 2 | 2 | 2 | 2 | 16 | 4 |
| 5h | 15√7 | |||
= | ||||
| 2 | 4 |
| 3√7 | ||
10h=15√7 ⇒ h= | ||
| 2 |
| 3√7 | 15√7 | |||
1) P=5x*h=5* | = | |||
| 2 | 2 |
| 15√7 | ||
=20*sinα | ||
| 2 |
| 3√7 | ||
15√7=40*sinα ⇒ sinα= | ||
| 8 |
| 63 | ||
cos2α=1− | ||
| 64 |
| 1 | ||
cos2α= | ||
| 64 |
| 1 | 1 | |||
|cosα|= | ⇒ cosα= | (ujemne rozwiązanie odrzucamy, ponieważ α∊(0o;90o)) | ||
| 8 | 8 |
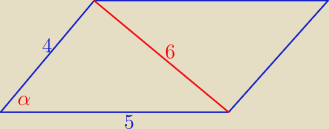 z tw. kosinusów
z tw. kosinusów
| 42+52−62 | ||
cosα= | = ........ | |
| 2*4*5 |
| 1 | ||
cosα = | ||
| 8 |




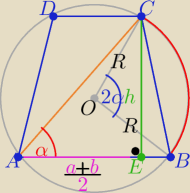 1/ rys.
2/ Napisz komentarze : jaki to musi być trapez, co powiesz o kącie BAC
1/ rys.
2/ Napisz komentarze : jaki to musi być trapez, co powiesz o kącie BAC
| a+b | ||
|AB|= | −−− dlaczego | |
| 2 |
| a+b | ||
|AE|= | ||
| 2 |
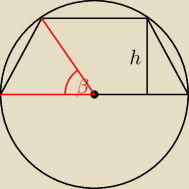 W takim razie kiedy narysowalibyśmy trapez wpisany w okrąg moim sposobem, a kiedy Twoim?
I czy moja interpretacja tego zadania mogłaby być prawidłowa? (β=2α)
W takim razie kiedy narysowalibyśmy trapez wpisany w okrąg moim sposobem, a kiedy Twoim?
I czy moja interpretacja tego zadania mogłaby być prawidłowa? (β=2α)
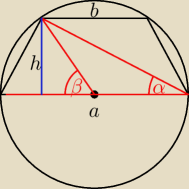 β=2α
β=2α
| (a+b)h | ||
P= | ||
| 2 |
| h | ||||||||
tgα= | ||||||||
|
| 2h | 2h | |||
tgα= | ⇒ a+b= | |||
| a+b | tgα |
| 1 | h | h2 | ||||
P= | *2* | *h= | , cnw. | |||
| 2 | tgα | tgα |

 Wniosek: nie jest ważne jak narysujesz ten trapez
Wniosek: nie jest ważne jak narysujesz ten trapez

 Dobranoc
Dobranoc
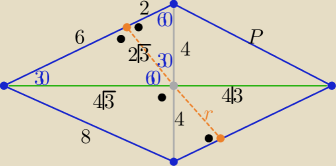 Zad3
P=32√3
======
Zad3
P=32√3
======
 Zadań mamy mnóstwo
Zadań mamy mnóstwo 

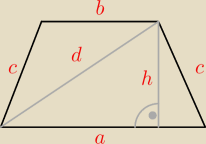 d=2√7
l − obwód trapezu
l=16
l=a+b+2c
stąd: c=4
w trapez można wpisać okrąg, zatem a+b=2c
h z twierdzenia Pitagorasa:
d=2√7
l − obwód trapezu
l=16
l=a+b+2c
stąd: c=4
w trapez można wpisać okrąg, zatem a+b=2c
h z twierdzenia Pitagorasa:
| a+b | ||
h2=d2−( | )2 | |
| 2 |
| (a−b)2 | ||
a+b=8 ∧ | =c2−h2 | |
| 22 |
| ⎧ | a+b=8 | |
| ⎩ | a−b=4 |
 Zad 6
Bok kwadratu ABCD ma długość 2. Na bku BC obrano punkt E, a na boku CD punkt F, taki że
Zad 6
Bok kwadratu ABCD ma długość 2. Na bku BC obrano punkt E, a na boku CD punkt F, taki że
| |CE| | |
=2. Przyjmując że |DF|=x, oblicz wartość x, dla której pole trójkąta AEF | |
| |DF| |
| 1 | ||
a) pole tego trapezu wyraża sie wzore P= | d2sin(2α) | |
| 2 |
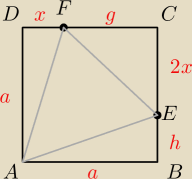 Zadanie 6
a=2
h=2−2x
g=2−x
PΔAEF=Pkw−PΔABE−PΔECF−PΔFDA
PΔAEF=4−2+2x−x(2−x)−x
PΔAEF=x2−x+2
niech P(x)=x2−x+2, x∊D=(0;1)
Zadanie 6
a=2
h=2−2x
g=2−x
PΔAEF=Pkw−PΔABE−PΔECF−PΔFDA
PΔAEF=4−2+2x−x(2−x)−x
PΔAEF=x2−x+2
niech P(x)=x2−x+2, x∊D=(0;1)
| 1 | ||
a=1>0, zatem wartość największa przyjmowana jest w x= | ∊D | |
| 2 |

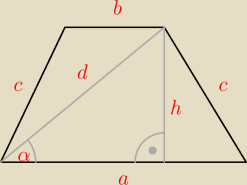 ad a
ad a
| (a+b)h | ||
P= | ||
| 2 |
| h | ||
sinα= | ⇒ h=d*sinα | |
| d |
| ||||||||
cosα= | ⇒ a+b=2d*cosα | |||||||
| d |
| 1 | 1 | |||
P= | *2d*cosα*d*sinα= | *d2*sin2α, cnw. | ||
| 2 | 2 |
| a+b | ||
cosα= | ||
| 2d |
| c | ||
cosα= | ⇒ c=d*cosα | |
| d |

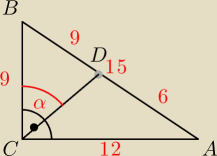 nie wiem jak dalej to ugryźć
wyznaczyłem wszystkie kąty za pomocą α i próbowałem z twierdzenia sinusów, ale coś nie mogę
złapać żadnej zależności odpowiedniej
nie wiem jak dalej to ugryźć
wyznaczyłem wszystkie kąty za pomocą α i próbowałem z twierdzenia sinusów, ale coś nie mogę
złapać żadnej zależności odpowiedniej
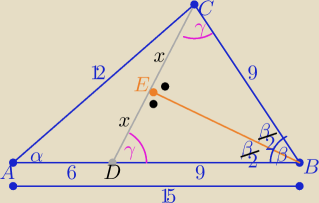
| 3 | 4 | |||
|AB|=15 cosβ= | i sinβ= | |||
| 5 | 5 |
| √5 | ||
1−cosβ= 2sin2(β/2) ⇒ ......... sin(β/2)= | ||
| 5 |
| √5 | ||
zatem cos(∡BCD)= | ||
| 5 |
| 9√5 | ||
WΔDBE : x=9*sin(β/2) ⇒x= | ||
| 5 |
| 18√5 | ||
to |DC|=2x= | ||
| 5 |
| x | 9√5 | |||
R= | ⇒ R= | |||
| sinβ | 4 |
| 1 | ||
P(ΔBCD)= | *9*9*sinβ | |
| 2 |
| 162 | ||
P= | ||
| 5 |
| 2P | ||
r= | ⇒ r=................. | |
| 9*9+2x |
| 18 | ||
r= | ||
| 5−√5 |


 bardzo ładnie Szkolniak
bardzo ładnie Szkolniak