Trójkąt 000: Bok AB trójkąta ABC ma długość 8. W tym trójkącie poprowadzono odcinek równoległy do AB który podzielił trójkąt na dwa obszary o równych polach. Długość tego odcina jest równa

Bogdan:

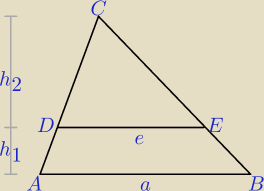
	P		a + e		P
Pole trapezu ABED:		=		* h1 ⇒ h1 =
	2		2		a + e

	P		e		P
Pole trójkąta DEC: =		=		* h2 ⇒ h2 =
	2		2		2

	a		a		P		P
Pole trójkąta ABC: P =		* (h1 + h2} =		* (		+		)
	2		2		a + e		2

	a
Po wykonaniu działań i uproszczeniu otrzymamy e =
	√2

Przypomina to podobne zagadnienie dla trapezu o podstawach a, b, w którym odcinek łączący ramiona trapezu i do nich równoległy rozcina trapez na dwa trapezy o równych polach. Ten odcinek jest równy średniej kwadratowej długości podstaw a, b. Jeśli w trójkącie przyjmiemy,

	a
że b = 0, to e = √(a2 + 02)/2 =
	√2

Tadeusz: a skala podobieństwa upraszcza to znacznie

Bogdan: Oczywiście Tadeuszu, upraszcza bardzo, pozdrawiam

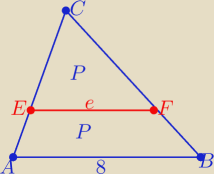
a@b: Z podobieństwa trójkątów ABC i EFC z cechy (kkk)

	2P
k2=		=2 ⇒ k=√2
	P

	8
k=		⇒...... e=4√2
	e