Przebieg zmienności funkcji Yop: Zbadaj przebieg zmienności funkcji f(x)=2x²/x+3 1. Dziedzina funkcji 2. Granice na krańcach określoności funkcji i asymptoty 3. Punkty przecięć z osiami układów współrzędnych 4. Własności specjalne − okresowość, parzystość, nieparzystość 5. Analiza pierwszej pochodnej − wypukłość, wklęsłość 6. Analiza drugiej pochodnej, wypukłość, wklęsłość, punkty przecięcia 7. Wykres funkcji

ABC: byś chociaż przepisał poprawnie, w pkt6 punkty przegięcia

Bleee: No to do dzieła. Wiesz co robić więc w czym problem?

Yop: @Bleee Gdybym wiedział jak i od czego zacząć to bym nie pisał zadania na forum.

ite: Pomysł, że wieczorem się wstawi zadanie, a rano znajdzie gotowy przebieg jej zmienności, to też przegięcie. f(x)=2x²/x+3=2x+3, x≠0 Wykresem jest prosta bez jednego punktu, więc przebieg nie jest specjalnie zaskakujący. Szczegóły badania tutaj http://matematykadlastudenta.pl/strona/261.html

Bleee: Człowieku.... Przecież podałeś punkty 'co trzeba zrobic'. Więc zaczyna się od punktu (1) i... określa się dziedzinę funkcji. A jeżeli nie wiesz jak się określa dziedzinę funkcji, to możesz spokojnie odpuścić sobie to zadanie i zacząć się oglądać za praca

Yop: @Bleee ogarnij się człowieku. Jak nie masz zamiar pomóc to po prostu nie pisz i nie śmieć w poście.

Yop: @ite dziękuję, tego potrzebowałem!

Blee: To TY się ogarnij. przyszedłeś, wrzuciłeś zadanie i czekasz jak święta krowa. Na pytanie: "w czym problem" odpowiadasz, że nie wiesz od czego zacząć −−− czyli nie rozumiesz treści zadania, bo byś wiedział że trzeba zacząć od wyznaczenia dziedziny. Jakbyś faktycznie chciał/−a pomocy (a nie gotowca) to byś napisał/−a co konkretnie jest problemem, a nie wstawił/−a zadanie i czekał/−a na rozwiązanie.

Blee: Takie zachowanie może i uchodziło Ci na sucho w liceum, ale na studiach nikt nie będzie się tym przejmować.

janek191:

	2 x2
Czy f(x) =		?
	x + 3

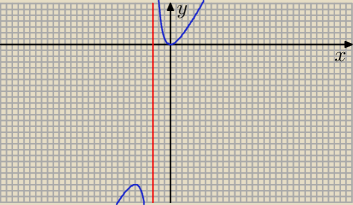
janek191: 1. D = ℛ \ { − 3} 2. lim f(x) = − ∞ x→ −∞ lim f(x) = +∞ x→ +∞ lim f(x) = −∞ x→ −3⁻ lim f(x) = +∞ x→ −3⁺ Asymptota pionowa: x = −3 3. Dla x = 0 f(0) = 0 Punkt przecięcia z osiami: P = ( 0,0) 4. Funkcja nie jest parzysta i nie jest nieparzysta. itd.