krótko i licze na szybką odpowiedz jaros: mógłby ktoś dla mnie wyprowadzić okres funkcji sin(x²)?

ABC: całki Fresnela ktoś kazał policzyć? to nie takie proste

Mila: Może y=sin²(x)

jaros: Nie nie chodzi dokładnie o sin(x²) jakby ktoś umiał nawet na całce to bym sie cieszył

jaros: znaczy chodzi po rpostu o okres bo nie wiem czy π to dobra odpowiedz

jc: To nie jest funkcja okresowa.

adelajda: ehhh chodzi o to, że w zadaniu jak dowiem sie jaki okres ma funkcja sin (x²) to już będe miał z górki

Blee: ale funkcja f(x) = sin(x²) NIE JEST funkcją okresową

jaros : to w takim razie co to jest

Blee: i się zdecyduj co do płci przynajmniej

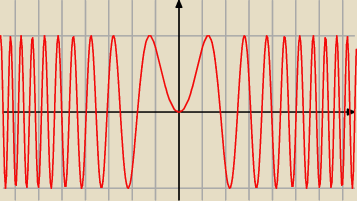
Blee: to jest funkcja jak widzisz ... im 'dalej' od początku osi tym wykres się coraz bardziej 'zagęszcza'

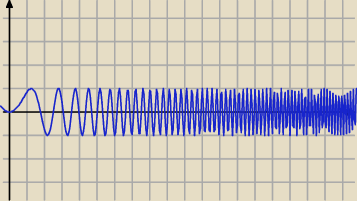
Blee: wersja dla x>0

Blee: pod koniec program rysujący już 'nie wyrabiał'

jaros : Widzę burza mózgów, badam ciągłość okresowość funkcji i wydaje mi się, że muszę znaleźć analogiczny wzór do t = 2Pi / b, b− liczba stojąca przed argumentem, przed arumentem stoi π/6, jakby patrzyć, badając ciąg dziedziną są liczby naturalne, a nie wszystkie rzeczywiste, więc jaki byłby wtedy okres takiej funkcju?

Blee: jeżeli masz f(n) = sin(n²) ; n∊N₊ to TYM BARDZIEJ nie jest to funkcja okresowa ... baaa ... jest to funkcja RÓŻNOWARTOŚCIOWA

jaros : Czy w zadniu chodzi o to by pokazać, że nie ma okresu podstawowego ciągu?

jaros : Bo tak rozumuje z tego co piszesz

Blee: nie wiem jaka jest treść zadania

jaros : Wyznacz okres podstawowy ciągu a_n=sin πx²/6, okresem podstawowym ciągu (a_n) nazywamy najmniejszą liczbę k∊N, dla której dla każdego n∊N, a_n=a_an+k

Bleee: A teraz popatrz jaka funkcje podałeś na początku To jest WIELKA ROZNICA.

jaros : W geogebrze wykresy są dość podobne

ABC: to że jest tam π i że bierzesz tylko liczby naturalne robi WIELKĄ różnicę

jaros : Sześć pierwszych wyrazów ciągu: sin(pi/6), sin(2pi/3), sin(3pi/2), sin(8pi/3), sin(25pi/6), sin(6pi) Argument ostatniego sinusa (i tylko ostatniego) jest parzystą wielokrotnością pi, czyli wartość tego sinusa wynosi 0. Jeżeli ciąg jest okresowy, to co pewną liczbę wyrazów musi się pojawiać 0 − tutaj jest sześć wyrazów i 0 pojawia się tylko raz, więc okres wynosi przynajmniej 6 i w każdym okresie pojawia się przynajmniej jedno 0. Sinus równa się zero wtedy i tylko wtedy, gdy jego argument jest parzystą wielokrotnością pi. Czyli mój ciąg ma zera tam, gdzie n²/6 jest liczbą parzystą. Zera tego ciągu pojawiają się co sześć wyrazów. Pozostaje pytanie: co się dzieje pomiędzy tymi zerami?

jaros : Wydaje mi się, że źle rozumiem polecenie

Bleee: a₁ = sin(π/6) a₂ = sin(4π/6) = sin(π/3) a₃ = sin(9π/6) = − sinπ a₄ = sin(16π/6) = sin(2π/6) = sin(π/3) a₅ = sin(25π/6) = sin(π/6) a₆ = sin(36π/6) = sin0 a₇ = sin(49π/6) = sin(π/6) = a₁ a₈ = a₂ a₉ = a₃ itd. zresztą sprawdź sam/−a

jaros : a₉=sin(81π/6) = sin(3π/2) = a₃ a₁0=sin(100π/6) = sin(2π/3) = a₄ Tzn, że okres podstawowy funkcji to 6?

Blee: nie ... to znaczy że masz PODEJRZENIE, że T = 6. Teraz musisz wykazać, że właśnie taki jest okres dla tego ciągu

jaros : Czyli co mam dokładnie zrobić?

Blee: dla jakiego najmniejszego t zachodzi równość:

	π		π
n2*		+ 2kπ = (n+t)2		; dla DOWOLNEGO (naturalnego) n i dla jakiegoś
	6		6

całkowitego k

jaros : Przekształcać to jakkolwiek?

Blee: tak i wnioskować z tego co otrzymasz

jaros : n²*π/6 +2kπ=(n²+2nt + t²)π/6 *6 n²*π +12kπ=(n²+2nt + t²)π ?

Blee: czyli 12kπ = π*t(2n + t) czyli 12k = t(2n + t) wnioskowanie

jaros : Czyli dla całkowitej liczby k i dla daolnego natrunalego n otrzymalismy okres jaki ta funckja przyjmuje?

Blee: k Ciebie NIE INTERESUJE ISTOTNE JEST t

jaros : podstawić za n i k 1 i obliczyć funkcje kwadratową?

jaros : hmmmm nie spotkałem sie jeszcze z takim dziwnym okresem ciągu... szczerze mówiąc to nie dokońca wiem, pogrupować t na jedna strone i n na drugą?

jaros : Ktoś wie jak pozbyć się T²?

Blee: 12k = t(2n+t) wnioskowanie 1) n jest zmienną więc (2n+t) jest zmienną 2) jeżeli t jest parzyste to 2n+t jest parzyste, więc podzielne przez 2 3) jeżeli t = 6 to t(2n+t) podzielne przez 12 4) więc mamy możliwości: t=2 , t=4 lub t=6 5) ale t musi być podzielne przez 3 ... (aby t(2n+t) było podzielne przez 12) ... więc t=6 koooniec wnioskowania

jaros: Czyli po zadaniu mam rozumieć, wykazaliśmy, ze okres jest równy 6