Trzy szybkie zadania optymalizacyjne Początkujący: 1. Dane są trapezy równoramienne o długościach ramion równych 6 cm i długości krótszej podstawy równej 6cm. Oblicz długość najdłuższej podstawy dla której pole jest największe. (pochodna wychodzi mi, że ma ekstremum w x=2, co nie jest zgodne z odpowiedziami) 2. Oblicz, jakie jest największe pole trójkąta prostokątnego, którego połowa obwodu jest równa p. (Nie mam pojęcia jak się do tego zabrać). 3. Analogiczne do 2 − Oblicz, który z trójkątów prostokątnych o danym polu P ma najmniejszy obwód. Proszę o pomoc, do momentu ułożenia funkcji, chciałbym się w końcu nauczyć tych zadań optymalizacyjnych...

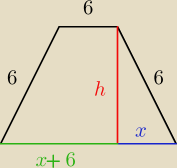
Saizou : Zad 1) Pitagoras h²+x²=36 h=√36−x²

	(6+6+2x)h
P(x, h) =		=(6+x)h
	2

P(x)=(6+x)√36−x²

Początkujący: Czy mógłbym Ciebie poprosić o policzenie z tego pochodnej dla sprawdzenia?

Saizou : Ja sobie ułatwię i wciągnę wszystko pod pierwiastek ...=√(6+x)²(36−x²) wymnóż to i wystarczy, że policzysz kiedy wyrażenie pod pierwiastkiem przyjmuje wartość największą

Początkujący: Z tego dostałem dwa pierwiastki x = 6 (nie należy do dziedziny) i x2 = −6 (też nie należy do dziedziny)

Saizou : Na pewno? Pokaż jaką masz funkcję pod pierwiastkiem i jej pochodną

Początkujący: Wyszło mi dobrze ostatecznie licząc pochodną funkcji złożonej Fakt, nie policzyłem tego pochodnej, wychodzi poprawnie, dzięki