Skąd to -1? kcmJ: Wyznacz najmniejszą i największą wartość funkcji f(x)=cos³x−cos2x+cos²x−cosx Korzystam z: cos2x=2cos²x−1 −cos2x=1−2cos²x Otrzymuję: f(x)=cos³x−cos²x−cosx+1 Wprowadzam zmienna pomocniczą t=cosx: f(x)=t³−t²−t+1 Liczę pochodną: f'(x)=3t²−2t−1 Delta: Δ=16 √Δ=4

	1
t1=−
	3

t₂=1 Liczę najmniejszą i największą wartość funkcji: f(1)=0

	1		5
f(−		)=1
	3		27

Wszystko jest dla mnie zrozumiałe, ale dlaczego w kluczu mam podane, że muszę jeszcze sprawdzić wartość f(−1)?

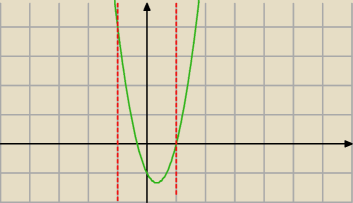
Blee: wykres f'(t) na czerwono zaznaczyłem założenia co t (t ∊ <−1 ; 1>) w t = −1/3 mamy maksimum lokalne w t = 1 mamy minimum lokalne funkcja f(t) będzie rosnąc na przedziale (−1 ; −1/3) więc skąd wiesz że dla t = 1 masz nie tylko minimum lokalne ale także minimum GLOBALNE (czyli że f(1) < f(−1)) Puki tego nie sprawdzisz, to nie wiesz o tym.

kcmJ: Już rozumiem. Zgadza się cosx <−1;1> zatem to są krańce przedziału, czyli sprawdzić krańce i ekstrema. Dziękuję ślicznie.