Maturalki
Saizou :
Kolejna porcja zadań dla maturzystów
(trochę liczb, trochę funkcji)
Zad 1
Liczba r jest najmniejszą liczbą rzeczywistą spełniającą nierówność
Podaj trzy pierwsze cyfry po przecinku rozwinięcia dziesiętnego liczby r.
Zad 2
Porównaj liczby a
b oraz b
a, gdzie
a=[(2−
√3)
1/2+(2+
√3)
1/2]
2
Zad 3
Wykaż, że dla dowolnej liczby naturalnej k liczba
k(k+1)(k+9)(k
2+1)
jest podzielna przez 5.
Zad 4
Dla jakiej wartości parametru m rozwiązaniem równania
|x−1|=m+2
jest para liczb o przeciwnych znakach?
Zad 5
Dla jakich wartości parametru m rozwiązaniem układu równań
jest para liczb (x, y) spełniająca nierówność |x−y|≤1
Zad 6
Suma dwóch różnych miejsc zerowych funkcji kwadratowej f jest równa 4,
| | 1 | |
a suma ich odwrotności jest równa − |
| . Wyznacz wzór tej funkcji, jeśli f(0)=−12. |
| | 3 | |
Zad 7
Rozwiąż równanie
a) (x
2−9)
√x−2=0
b)
√4x−7=x−1
Zad 8
Udowodnij, że dla każdej liczby rzeczywistej x i każdej liczby rzeczywistej m
prawdziwa jest nierówność
20x
2−20mx+18m
2≥4x+12m−5
8 sty 10:31
Szkolniak: Zadanie 1
|x−
√2|≤2
√2−2
x−
√2≥−2
√2+2 ∧ x−
√2≤2
√2−2
x≥2−
√2 ∧ x≤3
√2−2
x∊<2−
√2;3
√2−2>
Najmniejsza liczba to 2−
√2.
3 pierwsze cyfry: 585
8 sty 13:06
Saizou :
Zad 1

8 sty 13:12
Szkolniak: Zadanie 7
ad a
x∊D=<2;+
∞)
x
2−9=0 v
√x−2=p
x=−3 v x=3 v x=2
x∊{−3,2,3} ∧ x∊D
x∊{2,3}
ad b
Dla każdego x∊D obie strony równania są nieujemne, więc możemy podnieść obustronnie do
kwadratu:
4x−7=x
2−2x+1
x
2−6x+8=0
(x−4)(x−2)=0
x=4 v x=2
x∊[{2,4}]⊂D
8 sty 16:40
Saizou :
7 a) dobrze
7 b) zapis końca jest dziwny
x∊[{2,4}]⊂D
nie wiem co dla Ciebie miało to oznacza.
Lepiej napisać
| | 7 | |
(x=4 v x=2) ∧ x∊< |
| ; +∞) stąd x∊{2, 4} |
| | 4 | |
8 sty 17:14
Szkolniak: Zapis ten oznacza że zbiór rozwiązań równania zawiera się w dziedzinie, jest on niepoprawny?
8 sty 17:43
Saizou :
to po prostu x∊{2,4}⊂D
ten nawias kwadratowy jest zbędny i mylący
8 sty 17:44
Szkolniak: Ale gdybyśmy mieli sumę przedziałów, to wtedy używamy tego kwadratowego, dobrze myślę?
Typu x∊[(0;1)∪(1;2)]⊂D
8 sty 17:59
Saizou :
dla mnie ten zapis wygląda dosyć nienaturalnie (notabene przedziały
domkniętne oznacza się przez nawiasy kwadratowe w matematyce (tak są pisane książki zazwyczaj))
osobiście preferuje zapis
x∊(0;1)∪(1;2) ∧ x∊D zatem x ∊ ...
pokazujesz w ten sposób komisji, że należy wziąć część wspólną zbiorów
8 sty 18:25
Szkolniak: Rozumiem, dzięki wielkie za odpowiedź

8 sty 20:09
Saizou :
To teraz kolejne zadania czekają

8 sty 20:10
Szkolniak: Dam może innym szansę, bo chyba nie ma sensu pisać jak resztę umiem
8 sty 20:12
Saizou :
Czyli rozumiem że chcesz coś trudniejszego?
8 sty 20:14
Saizou :
Zad 9*
Rozwiąż nierówność
| | 3+√3 | |
limn→∞(1+tgx+tg2x+...+tgn−1x) ≤ |
| w zbiorze <0, 2π> |
| | 2 | |
8 sty 20:18
Saizou :
PS. Rozwiązywać zadania zawsze jest sens, chociażby po to aby poćwiczyć sprawność rachunkową.
8 sty 20:22
Szkolniak: Po lewej znajduje się suma ciągu geometrycznego, w którym a1=1, q=tgx, a ilość składników to
n?
8 sty 20:29
Saizou :
Tak, ale musisz pamiętać o tym, że granica ta musi istnieć
8 sty 20:33
Szkolniak: | | 1−tgnx | |
1+tgx+tg2x+...+tgn−1x= |
| |
| | 1−tgx | |
Przy liczeniu granicy pomoże mi teraz zamiana tangensa na iloraz sinusa i cosinusa?
I czy istnienie granicy związane jest z dziedziną tangensa?
8 sty 20:46
Saizou :
To nie jest potrzebne. Trzeba ustalić dla jakich wartości tangensa, ta granice istnieje.
Podpowiem że wiąże się to z szeregiem geometrycznym.
8 sty 20:48
Szkolniak: Granica istnieje jedynie wtedy, gdy |tgx|<1?
8 sty 20:52
Saizou :
Dokładnie tak. Granica skończona.
8 sty 20:55
Szkolniak: | | 1−tgnx | | limn→∞1−tgnx | | 1 | |
lim |
| = |
| = |
| |
| | 1−tgx | | limn→∞1−tgx | | 1−tgx | |
n→
∞
Jest okej?
8 sty 21:02
Saizou :
jest okej, ale tak
| | 1−tgnx | |
Sn = |
| to suma częściowa szeregu geometrycznego, przechodząc do granicy |
| | 1−tgx | |
mamy
8 sty 21:04
Szkolniak: W ogóle jest to zadanie z poziomu rozszerzonego?
Bo u mnie to tragedia czasami z tymi granicami jak patrzę na niektore przykłady, albo w
szkołach nie kładą na nie takiego wielkiego nacisku albo to u mnie przez nauczyciela
8 sty 21:08
Saizou :
granice w szkole to dosyć okrojony temat i zazwyczaj kończy się na schematycznym
ich rozwiązywaniu.
Na studiach poznasz wiele, wiele i wiele innych granic

Tak, to zadanie z kultowego zbioru Kiełbasy
8 sty 21:12
Szkolniak: Widzę przykład i właśnie widzę jaka przepaść między poziomem w szkole a powiedzmy tutaj

Ale spróbuję się i zobaczymy zaraz co z tego wyjdzie
8 sty 21:17
Saizou : Masz teraz nierównosc do rozwiązania
przy uwzględnieniu, że −1< tgx < 1
8 sty 21:23
Szkolniak: 1) |tgx|<1
tgx>−1 ∧ tgx<1
| | π | | π | |
x∊D=(− |
| +kπ; |
| +kπ), k∊C |
| | 4 | | 4 | |
| | 1 | | 3+√3 | |
2) |
| ≤ |
| /*2(1−tgx) |
| | 1−tgx | | 2 | |
2≤(1−tgx)(3+
√3), bo ⋀(1−tgx>0)
2≤3+
√3−3tgx−
√3tgx x∊D
| | π | | π | |
x∊<− |
| +kπ; |
| +kπ>, k∊C |
| | 6 | | 6 | |
Teraz wyciągamy część wspólną z 1) i 2):
| | π | | π | | π | | π | |
x∊(− |
| +kπ;− |
| +kπ>∪< |
| +kπ; |
| +kπ), k∊C |
| | 4 | | 6 | | 6 | | 4 | |
Jest okej?
I jeśli tak to jak się teraz odnieść do tego, że mamy to rozwiązać w zbiorze <0;2π>?
8 sty 21:37
Szkolniak: Mógłbym wszędzie dodać po π i pozbyć się dodania okresowości?
8 sty 21:39
Saizou :
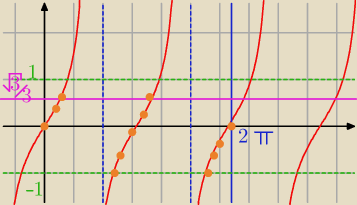
Część wspólna jest źle. Lepiej od razu odpowiedź z przedziału wypisać
(na rysunku te części z kropkami)
8 sty 21:54
Szkolniak: | | π | | π | |
Chwila chwila, część wspólna to przecież x∊<− |
| +kπ; |
| +kπ>, tak? |
| | 6 | | 6 | |
8 sty 22:04
Saizou :
Twoja cześć wspólna jest okej,
przepraszam, zasugerowałem się od razu okrojeniem do przedziału
8 sty 22:07
Szkolniak: Dopiero teraz widzę, że napisałeś, ale spytam tylko czy metoda rozwiązania jest okej,
przyjmując, że część wspólna to ta z 22:04

I teraz też mogę zrobić to w ten sposób, że będę podstawiał pod k kolejne liczby całkowite i
sprawdzał czy to się mieści w przedziale <0;2π>, tzn:
| | 5 | | 7 | |
1) dla k=1: x∊< |
| π; |
| π> |
| | 6 | | 6 | |
2) przesuwając się o kolejną (jedną) okresowość względem poprzedniego przedziału:
| | 11 | |
przedział ten nie mieści się cały, więc go 'ucinamy' i zostaje nam: x∊< |
| π;2π> |
| | 6 | |
| | 5 | | 7 | | 11 | |
odpowiedź końcowa: x∊< |
| π; |
| π>∪< |
| π;2π> |
| | 6 | | 6 | | 6 | |
dobrze?
8 sty 22:13
Patryk: Zadanie ze zbioru Kiełbasy

gdy je robiłem z założeniami bawiłem się dłużej niż z samym
| | pi | | 3 | | 7 | | 7 | |
liczeniem. Powinno wyjść x∊<0; |
| ∨ ( |
| pi; |
| pi) ∨ ( |
| pi; 2pi) |
| | 6 | | 4 | | 6 | | 4 | |
| | pi | | 3 | | 5 | | 7 | | pi | |
przy założeniu: x∊<0; |
| ) ∨ ( |
| pi; |
| pi) ∨ ( |
| pi; 2pi> i x≠ |
| i |
| | 4 | | 4 | | 4 | | 4 | | 2 | |
9 sty 01:49
Saizou :
Szkolniak część wspólna, to
| | π | | π | |
<− |
| +kπ; |
| +kπ> dla k ∊ ℤ (ℤ zbiór liczb całkowitych) |
| | 4 | | 6 | |
dla k =0
dla k = 1
dla k = 2
i uwzględniając przedział <0, 2π> otrzymujemy
| | π | | 3 | | 7 | | 7 | |
x∊<0, |
| > ∪ < |
| π; |
| π> ∪ < |
| π; 2π> |
| | 6 | | 4 | | 6 | | 4 | |
9 sty 10:36
Szkolniak: Dokładnie o to mi chodziło
Saizou
Możesz jeszcze jakimś przykładem rzucić jak masz coś pod ręką

9 sty 13:12
Saizou :
Zad 10*
Dla jakich wartości parametru a równanie
| | cosx | | cos2 | | cos3 | |
|
| + |
| + |
| +...=a2−2, |
| | 2 | | 4 | | 8 | |
którego lewa strona równania jest sumą nieskończonego ciągu geometrycznego ma rozwiązanie?
9 sty 14:11
Mila:
Brakuje argumentów

9 sty 15:51
salamandra: | cosx | | cos2x | | cos3x | |
| + |
| + |
| +...= a2−2 |
| 2 | | 4 | | 8 | |
|q|<1, bo zbiór wartości cosx <−1;1>
| | cosx2 | | cosx2 | | cosx | | 2 | |
S= |
| = |
| = |
| * |
| = |
| | 1−cosx2 | | | | 2 | | 2−cosx | |
Sama suma dobrze?
9 sty 16:16
Saizou :
@
Mila przy wpisywaniu się zjadły

Na razie jest dobrze
9 sty 16:22
salamandra: I teraz muszę przyrównać?
9 sty 16:30
9 sty 16:30
Saizou :
| | cosx | |
Znajdź zbiór wartości funkcji f(x)= |
| |
| | 2−cosx | |
9 sty 16:44
salamandra: Jedyne co wiem to ze cosx ∊ <−1;1>
Trzeba jakoś przekształcić wzór tej funkcji?
9 sty 16:49
Saizou :
Tak, należy przekształcić tak, aby było łatwo wyznaczyć zbiór wartości
9 sty 17:19
salamandra: Jakaś podpowiedź? nie mam pomysłu co wyciągnąć
9 sty 17:25
Saizou :
dodaj i odejmij 2 w liczniku
9 sty 17:25
salamandra: | cosx−2+2 | | −(2−cosx)+2 | |
| = |
| ? |
| 2−cosx | | 2−cosx | |
9 sty 17:36
Szkolniak: cosx=2a
2−4−a
2cosx+2cosx
a
2cosx−cosx=2a
2−4
| 2a2−4 | | 2a2−4 | |
| ≥−1 ∧ |
| ≤1 ∧ a≠1 ∧ a≠−1 |
| a2−1 | | a2−1 | |
Teraz wystarczy to rozwiązać i będzie ok?
9 sty 17:37
Mila:
Czas na planimetrię

9 sty 17:40
salamandra: | | 2a2−4 | |
Jak doszedłeś do postaci cosx = |
| , bo ja też tak zaczynałem robić, ale stanąłem |
| | a2−1 | |
właśnie linijkę przed wyznaczeniem cosx
9 sty 17:40
salamandra: @Mila lepiej nie

, od ponad miesiąca realizuję planimetrię na lekcji, nienawidzę tego działu

9 sty 17:41
Szkolniak: Wyciągasz po lewej stronie równania przed nawias cosx, w nawiasie zostaje Ci a
2−1

9 sty 17:41
salamandra: No przecież.....
9 sty 17:42
Szkolniak: U mnie też planimetria była swego rodzaju piętą achillesową, ale zacząłem coraz więcej zadań z
tego robić i już coraz lepiej jest

Także nie ma co myśleć że się nienawidzi działu, kwestia wytrenowania i będzie coraz łatwiejszy
9 sty 17:44
salamandra: No tam bardziej liczy się pomysł, zauważenie czegoś, a rozwiązanie to pigułka w tym wszystkim.
Najgorzej, że stereometria też przede mną, lepiej się czuję w algebrze.
9 sty 17:52
Saizou :
tylko jeszcze należy sprawdzić co się dzieje dla a=1 lub a =−1
9 sty 17:52
Saizou : Jak rozwiążecie zadania z tego wątku to wrzucę coś z planimetrii
9 sty 17:53
Szkolniak: Która jesteś klasa salamandra?
I dodatkowo co z warunkiem na q?
9 sty 17:55
salamandra: Ja na pewno zrobię te dopiero po weekendzie może, jutro i w poniedziałek mam ostatni egzamin
zawodowy i do tego na razie muszę przykuć uwagę

9 sty 17:55
salamandra: W 4−tej technikum
9 sty 17:55
Saizou :
Warunek był potrzebny aby szereg po lewej stronie był zbieżny
9 sty 18:03
Szkolniak: 1) Aby suma w ogóle istniała, musi zachodzić, że |q|<1, więc:
|cosx|<2 ⇒ x∊R
2) Dla a∊{−1,1} równanie przyjmuje postać 0=−2 i jest to równanie sprzeczne.
9 sty 18:08
Saizou :

Jeszcze pozostaje wyznaczyć parametr a.
Alternatywnie można
| | cosx | | cosx−2+2 | | −(2−cosx)+2 | |
f(x)= |
| = |
| = |
| = |
| | 2−cosx | | 2−cosx | | 2−cosx | |
9 sty 18:15
Adamm:
moim zdaniem, 8 sty 2020 20:18 zadanie jest źle przedstawione
nie dość, że np. tg(π/2) nie istnieje (a podajesz, żeby rozwiązać w [0, 2π]), to
w dodatku, sama granica może nie istnieć, i wtedy sama nierówność
nie ma sensu.
Poprawne sformułowanie zadania, byłoby by obliczyć tą nierówność, dla
x z przedziału [0, 2π] dla których tg(x) jest określony, i granica również istnieje
9 sty 18:15
Saizou :
@Adamm przepisałem to zadanie ze zbioru Kiełbasy.
Jeśli spojrzymy na to, że
Sn =1+tgx+...+tgn−1x
jest sumą częściową szeregu, to szereg jest zbieżny gdy istnieje granica
limn→∞ Sn
Przedział na końcu sugeruje, że chodzi o wybranie rozwiązań, które należą do tego zbioru.
Faktycznie mogłby być lepiej sformułowane to zadanie
9 sty 18:27
Szkolniak: Zadanie 5
2−2my=m+y
y+2my=2−m
| | 2−m | |
y(1+2m)=2−m ⇒ y= |
| |
| | 2m+1 | |
| | m(2−m) | | m(m−2) | | 2m+1+m2−2m | | m2+1 | |
x+my=1 ⇔ x=1− |
| ⇔ x=1+ |
| ⇔ x= |
| ⇔ x= |
| |
| | 2m+1 | | 2m+1 | | 2m+1 | | 2m+1 | |
|x−y|≤1
| | m2+1 | | 2−m | | 1 | |
| |
| − |
| |≤1 ∧ m∊D=R\{− |
| } |
| | 2m+1 | | 2m+1 | | 2 | |
| |m2+m−1| | |
| ≤1 /*|2m+1| |
| |2m+1| | |
|m
2+m−1|≤|2m+1|, bo ⋀(|2m+1|>0)
m∊D
| | 1 | | 1−√5 | | 1+√5 | |
1) (m2+m−1≥0 ∧ 2m+1≥0) ⇔ m∊D1=<− |
| ; |
| >∪< |
| ;+∞) |
| | 2 | | 2 | | 2 | |
m
2+m−1≤2m+1
m
2−m−2≤0
(m−2)(m+1)≤0
m∊<−1;2> ∧ m∊D
1
| | 1 | | 1−√5 | | 1+√5 | |
m∊<− |
| ; |
| >∪< |
| ;2> |
| | 2 | | 2 | | 2 | |
| | 1 | |
2) (m2+m−1≥0 ∧ 2m+1<0) ⇔ m∊D2=(−∞;− |
| ) |
| | 2 | |
m
2+m−1≤−2m−1
m
2+3m≤0
m(m+3)≤0
m∊<−3;0> ∧ m∊D
2
3) (m
2+m−1<0 ∧ 2m+1<0) ⇔ m∊∅
| | 1−√5 | | 1+√5 | |
4) (m2+m−1<0 ∧ 2m+1≥0) ⇔ m∊D4=( |
| ; |
| ) |
| | 2 | | 2 | |
−m
2−m+1≤2m+1
−m
2−3m≤0
m
2+3m≥0
m(m+3)≥0
m∊(−
∞;−3>∪<0;+
∞) ∧ m∊D
4
Sumując cztery przypadki:
| | 1−√5 | |
m∊<−3; |
| >∪<0;2> ∧ m∊D |
| | 2 | |
| | 1 | | 1 | | 1−√5 | |
m∊<−3;− |
| )∪(− |
| ; |
| >∪<0;2> |
| | 2 | | 2 | | 2 | |
I jak to wyszło?
9 sty 22:25
a@b:
O wiele uprasza rachunki
 |x−y|≤1 ⇔ x−y≤1 i x+y≥ −1
|x−y|≤1 ⇔ x−y≤1 i x+y≥ −1
| | m2+m−1 −2m−1 | |
1/ |
| ≤0 ⇒ (2m+1)(m2−m−2)≤0 ⇒ (2m+1)(m−2(m+1)≤0 |
| | 2m+1 | |
i
| | m2+m−1+2m+1 | |
2/ |
| ≥0⇒ (2m+1)m(m+3)≥0 |
| | 2m+1 | |
i m≠−1/2
dokończ ....................
9 sty 22:49
a@b:
Poprawiam zapis
W 1/ ................................... ⇒(2m+1)(m−2)(m+1)≤0
9 sty 22:52
a@b:
Odp: m∊<−3,−1> U <0,2>
======================
Może
Saizou potwierdzi

9 sty 22:57
a@b:
Widzę jeszcze chochlika ( sorry

Oczywiście ma być:
|x−y|≤1⇔ x−y≤1 i x−y≥ −1
9 sty 23:01
a@b:
No i
Szkolniak ... zaniemówił

9 sty 23:38
Szkolniak: A się rozpisałem niepotrzebnie

Twoje przedziały "ładniejsze", więc obstawiam że twoje dobrze

9 sty 23:54
a@b:
Wniosek: szanuj czas , bo na maturze
"czas droższy od pieniędzy" 
9 sty 23:59
Saizou : Potwierdzam wynik
Ety 
10 sty 10:33
Saizou :
Zadania 2, 3 4, 5, 8 jeszcze czekają na rozwiązanie
10 sty 10:35
Jerzy:
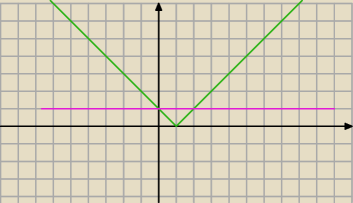
Zad. 4
m + 2 > 1 ⇔ m > − 1
10 sty 10:51
Saizou :

10 sty 12:29
a@b:
zad6
y=ax
2+bx+c
z treści zad f(0)=−12 ⇒
c= −12
ze wzorów Viete
'a
| | 1 | | 1 | | −b | | 1 | |
i |
| + |
| = |
| = − |
| ⇒ 3b=c ⇒ .... b=−4 to a=1 |
| | x1 | | x2 | | c | | 3 | |
y=x
2−4x−12
==========
10 sty 13:22
Szkolniak: Zadanie 2
a=2−
√3+2+2+
√3=6
b=...
81
−1=3
−4
√3=3
12
27
−2=3
−6
4√9=(3
2)
14=3
12
| | 3−4*312 | |
...= |
| =32=9 |
| | 3−6*312 | |
a
b czy b
a
6
9 czy 9
6
(6
3)
3 czy (9
2)
3
216
3 czy 81
3
zatem a
b>b
a
10 sty 13:43
Saizou :

dla
Ety oraz

dla
Szkolniaka
10 sty 15:23
Saizou :
Pozostały dowody

10 sty 20:18
a@b:
zad3/
k(k+1)[(k−1)+10][(k
2−4)+5]= k(k+1)[[(k−1)+10][(k−2)(k+2)+5]=
po wymnożeniu
(k−2)(k−1)k(k+1)(k+2)+
5k(k+1)(k−1)+
10k(k+1)(k−2)(k+2)+
50k(k+1)
dodać odpowiedni komentarz
i po b
ólu

10 sty 21:56
Saizou :
Ładnie, można też sprawdzać liczby postaci 5k, 5k+1, 5k+2, 5k+3, 5k+4
wtedy wychodzi z automatu

10 sty 21:59
a@b:
Wiem

Ja wolę tak , jak podałam

10 sty 22:00
Saizou :
Wiem

Mam jeszcze w pamięci dowód podzielności n
5−n przez 30

10 sty 22:02
a@b:

10 sty 22:03
Saizou :
Zostaje ostanie.
Trochę słabo, że chętnych maturzystów brakuje
10 sty 22:05
a@b:
Czyszczą garnitury na studniówką

10 sty 22:05
ite: Raczej ćwiczą przysiady do kroku poloneza.
10 sty 22:07
a@b:
Może przelewają "napoje wyskokowe" do kartonów po mleku

10 sty 22:08
ite: po soku i coli
tradycja...
10 sty 22:09
Saizou :
Haha, na zdrowie

10 sty 22:10
salamandra: Akurat na zdrowie

tak jak mówiłem, ja ruszę z zadaniami od poniedziałku. Miłego weekendu
wszystkim
10 sty 22:19
a@b:
Trzymamy za słowo

Miłego.....
10 sty 22:21
Szkolniak: W ostatnim zadaniu nie wystarczy przerzucić wszystkiego na lewą stronę i wykazać, że jeśli
a=20>0, to Δ≤0, żeby nierówność była zawsze spełniona?
10 sty 22:25
Saizou :
Wystarczy

+ komentarz
10 sty 22:27
a@b: 
10 sty 22:30



 Tak, to zadanie z kultowego zbioru Kiełbasy
Tak, to zadanie z kultowego zbioru Kiełbasy
 Ale spróbuję się i zobaczymy zaraz co z tego wyjdzie
Ale spróbuję się i zobaczymy zaraz co z tego wyjdzie
 Część wspólna jest źle. Lepiej od razu odpowiedź z przedziału wypisać
(na rysunku te części z kropkami)
Część wspólna jest źle. Lepiej od razu odpowiedź z przedziału wypisać
(na rysunku te części z kropkami)
 I teraz też mogę zrobić to w ten sposób, że będę podstawiał pod k kolejne liczby całkowite i
sprawdzał czy to się mieści w przedziale <0;2π>, tzn:
I teraz też mogę zrobić to w ten sposób, że będę podstawiał pod k kolejne liczby całkowite i
sprawdzał czy to się mieści w przedziale <0;2π>, tzn:
 gdy je robiłem z założeniami bawiłem się dłużej niż z samym
gdy je robiłem z założeniami bawiłem się dłużej niż z samym


 Na razie jest dobrze
Na razie jest dobrze

 , od ponad miesiąca realizuję planimetrię na lekcji, nienawidzę tego działu
, od ponad miesiąca realizuję planimetrię na lekcji, nienawidzę tego działu


 Także nie ma co myśleć że się nienawidzi działu, kwestia wytrenowania i będzie coraz łatwiejszy
Także nie ma co myśleć że się nienawidzi działu, kwestia wytrenowania i będzie coraz łatwiejszy

 Jeszcze pozostaje wyznaczyć parametr a.
Alternatywnie można
Jeszcze pozostaje wyznaczyć parametr a.
Alternatywnie można
 |x−y|≤1 ⇔ x−y≤1 i x+y≥ −1
|x−y|≤1 ⇔ x−y≤1 i x+y≥ −1

 Oczywiście ma być:
|x−y|≤1⇔ x−y≤1 i x−y≥ −1
Oczywiście ma być:
|x−y|≤1⇔ x−y≤1 i x−y≥ −1

 Twoje przedziały "ładniejsze", więc obstawiam że twoje dobrze
Twoje przedziały "ładniejsze", więc obstawiam że twoje dobrze 


 Zad. 4
m + 2 > 1 ⇔ m > − 1
Zad. 4
m + 2 > 1 ⇔ m > − 1

 dla Ety oraz
dla Ety oraz  dla Szkolniaka
dla Szkolniaka



 Ja wolę tak , jak podałam
Ja wolę tak , jak podałam 
 Mam jeszcze w pamięci dowód podzielności n5−n przez 30
Mam jeszcze w pamięci dowód podzielności n5−n przez 30 




 tak jak mówiłem, ja ruszę z zadaniami od poniedziałku. Miłego weekendu
wszystkim
tak jak mówiłem, ja ruszę z zadaniami od poniedziałku. Miłego weekendu
wszystkim
 Miłego.....
Miłego.....
 + komentarz
+ komentarz
