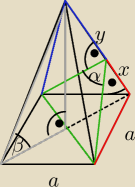
 k − krawędź boczna
d − przekątna kwadratu
H − wysokość ostrosłupa
d=a√2
y=k−x
a=√6
z trójkąta zielonego obliczamy długości wysokości ścian bocznych oznaczone literą h:
k − krawędź boczna
d − przekątna kwadratu
H − wysokość ostrosłupa
d=a√2
y=k−x
a=√6
z trójkąta zielonego obliczamy długości wysokości ścian bocznych oznaczone literą h:
| √3 | ||
sin60°= | ||
| h |
| √3 | √3 | |||
= | ⇒ h=2 | |||
| 2 | h |
| 3 | ||
2k=3√2 ⇒ k= | √2 | |
| 2 |
| d | ||
( | )2+H2=k2 | |
| 2 |
| 18 | ||
3+H2= | ||
| 4 |
| 3 | √6 | |||
H2= | ⇒ H= | |||
| 2 | 2 |
| ||||||||
cosβ= | ||||||||
| k |
| d | ||
cosβ= | ||
| 2k |
| 2√3 | ||
cosβ= | ||
| 3√2 |
| √6 | ||
cosβ= | ⇒ β≈35° | |
| 3 |
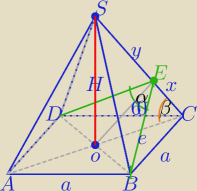 α=120o, BE⊥SC i DE⊥SC
a=√6
1) |DB|=√6*√2=√12=2√3
|OB|=√3
α=120o, BE⊥SC i DE⊥SC
a=√6
1) |DB|=√6*√2=√12=2√3
|OB|=√3
| OB | √3 | |||
tg60= | ⇔√3= | ⇔|OE|=1, |BE|=2 | ||
| OE | |OE| |
| 3 | ||
2H2=3, H2= | ||
| 2 |
| √6 | ||
H= | ||
| 2 |
| H |
| |||||||||
4) tgβ= | ⇔ tgβ= | |||||||||
| OC| | √3 |
| √2 | ||
tgβ= | ||
| 2 |
