grafy mat123: Rozstrzygnij czy istnieje graf, który jest jednocześnie eulerowski i hamiltonowski oraz ma: a. nieparzystą liczbę wierzchołków i nieparzystą liczbę krawędzi b. nieparzystą liczbę wierzchołków i parzystą liczbę krawędzi c. parzystą liczbę wierzchołków i nieparzystą liczbę krawędzi d. parzystą liczbę wierzchołków i parzystą liczbę krawędzi Bardzo proszę o pomoc.

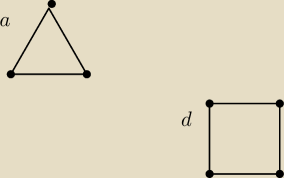
Blee: czyli czy istnieje graf który ma taką ścieżkę że dokładnie raz przechodzisz przez wszystkie wierzchołki oraz ścieżkę że dokładnie raz przechodzisz przez wszystkie krawędzie

mat123: Czyli w b i c odpowiedź będzie negatywna?

Blee: jeżeli to musisz pokazać dlaczego będzie negatywna odpowiednie twierdzenia trzeba odnaleźć

mat123: Czy wystarczy powołać się na to, że aby istniał graf eulerowski to stopnie każdego wierzchołka muszą być liczbami parzystymi, a w tych przypadkach jest to niemożliwe?

Blee: dokładnie oto chodzi

mat123: Dziękuję bardzo za pomoc