Kilka zadań z matematyki, proszę o pomoc mmmstd: hej, pomoże ktoś? 1.Rozwiąż nierówność:

	1
		− 1 > tg x
	cos2 x

√3 · 3^−x < 9 log₂(3 − 2x) − log₂(4x − 1) < 1 2. Rozwiąż równanie:

	√3
cos x =
	2

3.Pomiędzy liczby 24 i 4 wstaw dwie liczby w taki sposób, aby trzy pierwsze utworzyły ciąg arytmetyczny, a trzy ostatnie – ciąg geometryczny. 4.Naszkicuj wykres funkcji f. Określ jej dziedzinę i zbiór wartości, wyznacz miejsca zerowe, omów monotoniczność f(x) = 2^x + 3

Jerzy: 1) 3^{1/2 − x} < 3² , dalej potrafisz ?

mmmstd: Tak, dziękuję, czekam za resztą

Szkolniak: 3) zapiszmy szukany ciąg jako (24,x,y,4) z własności ciągu arytmetycznego: 2x=24+y z własności ciągu geometrycznego: y²=4x

⎧	4x=48+2y
⎩	y2=4x

y²=48+2y y²−2y−48=0 (y−8)(y+6)=0 y=8 v y=−6 przypadek 1: y=8 ⇒ x=16 ciąg ma postać (24,16,8,4) przypadek 2: y=−6 ⇒ x=9 ciąg ma postać (24,9, −6, 4)

mat123: 1. c)

	3−2x
log2		< log20
	4x−1

log₂x jest funkcją różnowartościową rosnącą zatem otrzymujemy:

3−2x
	< 0
4x−1

i teraz rozwiązujesz zwykłą nierówność oczywiście wcześniej musisz wyznaczyć dziedzinę 2. x₀ = ^π₆ x = x₀ + 2kπ v x = −x₀ + 2kπ

Szkolniak: 4) f(x)=2^x+3 a) dziedziną funkcji jest zbiór liczb rzeczywistych b) zbiór wartości wykres funkcji f jest przesunięty o 3 jednostki w górę względem pierwotnej funkcji

	2
y=		, której zbiorem wartości jest przedział (0;+∞), więc zbiorem wartości 'nowej'
	x

funkcji będzie przedział (3;+∞) c) miejsca zerowe 2^x+3=0 2^x=−3 sprzeczność, brak miejsc zerowych d) funkcja jest rosnąca w całej swojej dziedzinie

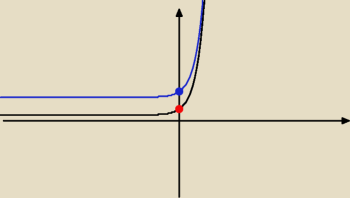
mat123: 4. f(x) to nic innego jak wykres g(x) = 2^x przesunięty o wektor v=[0, 3] (3 jednostki w górę). czerwony punkt: (0,1) niebieski (0,3)

mmmstd: Dziękuję bardzo, zostało jeszcze 1a do wyjaśnienia mi

Des: Dobrze przepisałeś?

mmmstd:

1
	− 1 > tg x
cos2x

Des:

1 − cos2x
	> tgx
cos2x

sin2x + cos2x − cos2x
	> tgx
cos2x

sin2x
	> tgx
cos2x

tg²x > tgx tgx( tgx − 1) > 0 ...

Szkolniak: + dziedzina

Jerzy: Lewą stronę sprowadź do wspólnego mianownika i wykorzystaj: 1− cos²x= sin²x