Zadania maturalne
Saizou :
Cześć, postanowiłem że co jakiś czas będę wrzucać zadania przygotowujące do matury
na poziomie rozszerzonym, chętnych licealistów/techników zapraszam do rozwiązywania
a osoby pomagające proszę o udzielanie wskazówek lub podanie pomysłu, ale nie gotowca
(to w sytuacji, gdy ktoś już na prawdę nie będzie wiedział co i jak).
Zaczynamy od działu: Liczby, zbiory i wartość bezwzględna.
Zad 1
| | 2x | | y | |
Wykaż, że dla x>0 i y>0 zachodzi nierówność |
| + |
| ≥ 0. |
| | y | | 2x | |
Zad 2
Uzasadnij, że suma pięciu kolejnych liczb podzielnych przez 3 jest podzielna przez 15.
Zad 3
Wyznacz wszystkie pary liczb całkowitych a i b, dla których a
2−b
2=15
Zad 4
Rozwiąż równanie
|2x+2|+3x=|x|+2
Zad 5
Rozwiąż nierówność
|x+5|−|x−2|≤3
Zad 6
Zaznacz w układzie współrzędnych zbiór rozwiązań nierówności
|y| ≤ |x−1|
Zad 7
Wykaż, że liczba
3√√5+2−
3√√5−2 jest całkowita
Zad 8
Uzasadnij, że dla dowolnych różnych liczb rzeczywistych x i y prawdziwa jest nierówność
(x+1)(x+2)+(y+1)(y+2)+1≥(x+2)(y+2)
Zad 9
Dane jest równanie |mx|+|m|=4, w którym x jest niewiadomą.
a) rozwiąż równanie dla m=2
b) Dla jakich wartości parametru m równanie ma rozwiązanie.
Zad 10
Wykaż, że dla każdej liczby naturalnej k liczba (k
3+k
2)(k
2+3k+2)(k+2) jest podzielna przez
36
Na razie tyle

6 sty 16:03
a@b:


6 sty 16:03
Saizou :
Eta nudzi mi się więc postanowiłem coś porobić produktywnego

6 sty 16:07
a@b:
Bardzo dobry pomysł

6 sty 16:09
Saizou :
Ciekawe czy ktoś się skusi

6 sty 16:10
salamandra: Dzięki, na pewno się podejmę

6 sty 16:11
Saizou : To czekamy na rozwiązania

6 sty 16:14
a@b:
Czasy kiedy
Godzio,
ICSP ,
Saizou,
bezendu.
Metis,
Blue,
Kejt,
kyrtap ,
Metis i inni ....oraz nawet tacy, jak
macio 
.
pilnie tu na forum przygotowywali się do matury (z naszą pomocą )
bezpowrotnie minęły ! ( a szkoda

6 sty 16:17
salamandra: zad1.
| 2x | | y | |
| + |
| ≥ 0 / *y (y>0) więc nie zmieniam znaku nierówności, przekształcenie jest |
| y | | 2x | |
równoważne
| | y2 | |
2x+ |
| ≥ 0 / *2x (tak samo jak wyżej) |
| | 2x | |
4x
2+y
2 ≥ 0
Przekształciłem równoważnie nierówność, a wniosek z ostatniej linijki jest taki, że suma dwóch
dodatnich składników jest zawsze dodatnia,
c.n.u
6 sty 16:17
a@b:
..."jest zawsze dodatnia"? czy zawsze ....
6 sty 16:19
Saizou :
To prawda

Twoje rozumowanie w tym przykładzie jest słuszne

źle przepisałem, miało być
6 sty 16:19
a@b:
@
salamandra czy zero jest dodatnie ?

6 sty 16:21
salamandra: Liczby podzielne przez 3 określam wzorem 3n, gdzie n∊ C/N (mam dylemat)
kolejne: (3n, 2*3n, 3*3n, 4*3n, 5*3n)
3n+6n+9n+12n+15n = 45n
45n jest podzielne przez 15., ponieważ 45/15 = 3, więc n nas nie ogranicza.
6 sty 16:22
salamandra: @a@b
Ale x i y > 0, więc zero nie wchodzi w grę?

6 sty 16:23
Szkolniak: To może ja zacznę

| | 2x | |
Z1) x,y>0 i niech a= |
| >0 |
| | y | |
a
2+1≥2a, bo a>0
a
2−2a+1≥0
(a−1)
2≥0
Kwadrat dowolnej liczby rzeczywistej jest liczbą nieujemną, zatem powyższa nierówność jest
zawsze spełniona.
6 sty 16:23
Saizou :
źle, to nie są kolejne liczby podzielne przez 3
np. dla n = 2 mamy
6, 12, 18 ...
musisz to inaczej zapisać
Co do n, to jest całkowite.
6 sty 16:24
a@b:
Kolejne liczby podzielne przez 3:
3n−6, 3n−3,3n, 3n+3, 3n+6,........
6 sty 16:24
salamandra: czy jest jakiś ogólny wzór na kolejne liczby podzielne przez n? Czy trzeba to po prostu
wydedukować?
6 sty 16:26
salamandra: w takim razie
3n−6+3n−3+3n+3n+3+3n+6 = 15n = 15*n <− jest podzielne przez 15, o to chodziło?
6 sty 16:28
Saizou :
Jest, ale po co? Lepiej dedukować.
np. kolejne liczby podzielne przez 7, to
7k, 7k+7, 7k+14 itd.
trzy kolejne liczby, które przy dzieleniu przez 5 dają resztę 2 to
5k+2, 5k+7, 5k+12
6 sty 16:28
salamandra: Aha, czyli idąc moim "wzorem" to po prostu powinienem był zapisać 3n, 3n+3 itd?
6 sty 16:30
Saizou :
Zad. 2
 Szkolniak
Szkolniak + komentarz o przekształceniach równoważnych i będzie super
6 sty 16:31
albi: Ciężko tu mówić o wzorze ogólnym, po prostu odległość kolejnych liczby podzielnych przez jakąś
liczbę to ta liczba
6 sty 16:31
Saizou :
salamandra tak. spróbuj dla siebie to zrobić z liczbami
3n, 3n+3, itd.
6 sty 16:32
salamandra: 3n+3n+3+3n+6+3n+9+3n+12 = 15n+30 = 15(n+2) <− podzielne przez 15
6 sty 16:33
Saizou :
super

6 sty 16:33
salamandra: Trzeciego przyznam, że w ogóle nie potrafie zacząć
6 sty 16:34
Saizou :
zastosuj wzór x2−y2=(x−y)(x+y)
i teraz rozłóż 15 na iloczyn dwóch liczb i zrób odpowiednie układy równań
6 sty 16:35
Jerzy:
(a + b)(a − b) = 15 , teraz rozpatruj możliwości.
6 sty 16:37
salamandra: no właśnie jedyne co zrobiłem to rozłożyłem na (a−b)(a+b)

Czyli (a−b)(a+b) = 3*5 ⇔ a−b = 3 ⋀ a+b = 5?
I potem brać inne pary? np. 5*3, 1*15, 15*1?
6 sty 16:37
a@b:
Jeszcze:
(−1)*(−15)=(−3)*(−5)
6 sty 16:38
Jerzy:
Pamiętaj o ujemnych czynnikach.
6 sty 16:38
Saizou :
Tak, pamiętając, że mogą być też wersje z minusami
6 sty 16:38
Jerzy:
Tutaj kolejność czynników też ma znaczenie.
6 sty 16:39
salamandra: Wiem, dlatego wypisałem też 5*3
6 sty 16:40
Szkolniak: Zadanie 4)
|2x+2|+3x=|x|+2
2|x+1|+3x=|x|+2
1° x∊D1=(−∞;−1)⇒(|x+1|=−x−1 ∧ |x|=−x)
−2(x+1)+3x=−x+2 ∧ x∊D1
−2x−2+3x=−x+2
2x=4
x=2∉D1
v2° x∊D2=<−1;0)⇒(|x+1|=x+1 ∧ |x|=−x)
2x+2+3x=−x+2 ∧ x∊D2
6x=0
x=0∉D2
v3° x∊D3=<0;+∞)⇒(|x+1|=x+1 ∧ |x|=x)
2x+2+3x=x+2 ∧ x∊D3
4x=0
x=0∊D3
Zatem jedynym rozwiązaniem jest liczba 0.
6 sty 16:44
Saizou :
Dobrze

6 sty 16:48
Szkolniak: Dobra, jeszcze 9−te i starczy

|mx|+|m|=4
ad a
m=2 ⇒ |2x|+2=4
2|x|=2
|x|=1
x=−1 v x=1
x∊{−1,1}
ad b
|mx|+|m|=4
|m|*|x|+|m|=4
|m|(|x|+1)=4
| | 4 | |
Równanie to ma rozwiązanie wtedy, gdy |
| −1≥0: |
| | |m| | |
4≥|m|, bo ⋀(|m|>0)
m∊D
|m|≤4
m∊<−4;4> ∧ m∊D
m∊<−4;0)∪(0;4>
6 sty 16:57
salamandra: zad3.
1) (a−b)(a+b) = 3*5
a−b=3
a+b = 5
a= 3+b
3+b+b = 5
2=2b
b=1
a= 4, b = 1
========
2) (a−b)(a+b) = 5*3
a−b=5
a+b = 3
a= 5+b
5+b+b = 3
−2=2b
b=−1
a= 4, b = −1
========
3)
(a−b)(a+b) = −5*(−3)
a−b=−5
a+b = −3
a= −5+b
−5+b+b = −3
2=2b
b=1
a= −5, b = 1
========
4)
(a−b)(a+b) = −3*(−5)
a−b=−3
a+b = −5
a= −3+b
−3+b+b = −5
−2=2b
b=−1
a= −4, b = −1
========
5)
(a−b)(a+b) = 1*15
a−b=1
a+b = 15
a= 1+b
1+b+b = 15
14=2b
b=7
a= 8, b = 7
========
6)
(a−b)(a+b) = 15*1
a−b=15
a+b = 1
a= 15+b
15+b+b =1
−14=2b
b=−7
a= 8, b = −7
========
7)
(a−b)(a+b) = −1*(−15)
a−b=−1
a+b = −15
a= −1+b
−1+b+b = −15
−14=2b
b=−7
a= −8, b = −7
========
8)
(a−b)(a+b) = −15*(−1)
a−b=−15
a+b = −1
a= −15+b
−15+b+b = −1
14=2b
b=7
a= −8, b = 7
========
6 sty 17:06
Saizou :
bardzo dobrze

6 sty 17:07
Saizou :
w 3) układzie masz błąd rachunkowy, ale reszta jest okej
6 sty 17:08
salamandra: a=−4 fakt+
6 sty 17:10
salamandra: 4.
1. x∊ <−∞; −1)
−(2x+2)+3x = −x+2
−2x−2+3x+x−2 = 0
2x= 4
x = 2
2. x∊ <−1; 0)
2x+2+3x= −x+2
6x =0
x=0
3. x∊ <0; ∞)
2x+2+3x=x+2
5x+2 = x+2
x= 0
6 sty 17:13
Saizou :
Czyli jaka jest odpowiedź w 4?
Bo nigdzie nie uwzględniłeś przedziałów, w których zostały rozwiązywane równania
6 sty 17:16
salamandra: No tak, ostatni raz z takimi równaniami miałem do czynienia 3 lata temu (w 1 klasie), wyszedłem
z wprawy

w 1. przedziale x nie nalezy do dziedziny.
w 2 również, gdyż przedział otwarty.
więc x=0 to rozwiązanie., bo tylko w trzecim nalezy do przedziału.
6 sty 17:19
salamandra: 5.
1. x∊ (−∞; −2)
x+5−[−(x−2)] ≤ 3
x+5 − (−x+2) ≤ 3
2x+3 ≤ 3
2x ≤ 0
x ≤ 0
więc x∊(−∞; −2)
2. x∊ <−2; ∞)
x+5−(x−2) ≤ 3
7≤3
x∊ ∅
6 sty 17:22
Saizou :
I teraz jest dobrze

Warto pamiętać o takich rzeczach, żeby punkty na maturze nie leciały
6 sty 17:22
salamandra: ups. zapomniałem jednego przedziału, sekunda
6 sty 17:24
Saizou :
W przedziale x∊(−∞, −2) nie określisz znaku wyrażenia |x−2|
6 sty 17:24
salamandra: dlaczego?
6 sty 17:27
salamandra: raczej |x+5|
6 sty 17:28
Saizou :
Nie to wyrażenie skopiowałem, miało być |x+5|
dla x=−3 mamy |−3+5|=|2|
a dla x=−10 mamy |−10+5|=|−5|
6 sty 17:29
salamandra: oczywiście chodziło o (−∞; 2), nie wiem skąd wziąłem ten minus
6 sty 17:30
salamandra: ale to też źle
przedziały które badam to
(−∞; −5)
<−5; 2)
<2; ∞)
6 sty 17:30
Saizou :
Tak, wiec napisz raz jeszcze rozwiązanie

6 sty 17:32
salamandra: 1. x∊ (−∞; −5)
−x−5−[−(x−2)] ≤ 3
−x−5−(−x+2) ≤ 3
−x−5+x−2 ≤ 3
−7≤3
x∊ R
suma zbioru: x∊ (−∞; −5)
2. x∊ <−5; 2)
x+5−[−(x−2)] ≤ 3
x+5+x−2 ≤ 3
2x+3 ≤ 3
x≤ 0
suma zbioru: x∊ <−5;0>
3. x∊ <2; ∞)
x+5−(x−2) ≤ 3
7≤ 3
x∊∅
I teraz nie wiem, jak zsumować te zbiory, w sensie, czy wziąć (−∞; 0>, czy brak rozwiązania−
czy jest to LUB to, czy musi być to ORAZ to.
6 sty 17:37
Saizou :
Po 1) nie możesz pisać suma zbiorów przy przypadkach, gdy sprawdzasz czy rozwiązanie
należy do przedziału − jest to iloczyn przedziałów.
Po 2) na końcu bierzesz sumę, bo rozbiłeś wszystkie liczby rzeczywiste na przypadki,
i teraz musisz to poskładać. (gdybyś brał iloczyn, to masz iloczyn zbioru pustego
z czymkolwiek, to jest to zbiór pusty)
6 sty 17:43
Szkolniak: W poszczególnych przypadkach wyciągasz część wspólną twojej nierówności i dziedziny w danym
przypadku.
Natomiast na sam koniec sumujesz przedziały ze wszystkich przypadków
6 sty 17:45
salamandra: Nie wiedziałem jak to ubrać w słowa, po prostu w tej mojej "sumie" uwzględniałem jeszcze
dziedzinę, czyli na końcu "dodaję" te przedziały, czyli
biorę
(−∞; −5) oraz <−5;0> i z tego wychodzi x∊ <−∞; 0>?
6 sty 17:46
Szkolniak: Tak
6 sty 17:49
Saizou :
Tak

6 sty 17:50
Szkolniak: Jak już salamandra tak leci to pomogę i z kolejnym

8) x,y∊R ∧ x≠y
Przekształcam równoważnie daną nierówność:
(x+1)(x+2)+(y+1)(y+2)+1≥(x+2)(y+2)
x
2+3x+2+y
2+3y+2+1≥xy+2x+2y+4
x
2+3x+y
2+3y≥xy+2x+2y
x
2+x+y
2+y−xy≥0 /*2
2x
2−2xy+2y
2+2x+2y≥0
x
2−2xy+y
2+x
2+2x+y
2+2y≥0
(x−y)
2+(x+1)
2+(y+1)
2≥2
x−y≥0
x+1≥1
y+1≥1
zatem suma ich kwadratów jest na pewno większa lub równa 2, cnw.
Jest okej?
6 sty 17:52
salamandra: Następnego nie wiem jak zacząć

6 sty 17:53
Szkolniak: salamandra, musisz rozpatrzeć cztery przypadki:
1) y≥0 ∧ x−1≥0
2) y≥0 ∧ x−1<0
3) y<0 ∧ x−1≥0
4) y<0 ∧ x−1<0
narysuj układ współrzędnych i dla każdego przypadku rozwiąż graficznie w odpowiednich
przedziałach nierówność liniową
6 sty 17:58
Saizou :
Szkolniaku zgubiłeś 1 w upraszczaniu wyrażeń w 3 linijce
samanadra zobacz jak to będzie wyglądać dla y≥0 i dla y<0 (będą to funkcje 'liniowe' z
wartością bezwzględną)
6 sty 17:59
Szkolniak: 8) poprawka*
(x+1)(x+2)+(y+1)(y+2)+1≥(x+2)(y+2)
x
2+3x+2+y
2+3y+2+1≥xy+2x+2y+4
x
2+3x+y
2+3y+1≥xy+2x+2y
x
2+x+y
2+y+1−xy≥0 /*2
2x
2−2xy+2y
2+2x+2y+2≥0
(x−y)
2+(x+1)
2+(y+1)
2≥0
teraz okej

6 sty 18:15
Saizou :
+ komentarz dlaczego składniki są nieujemne
6 sty 18:19
salamandra: Funkcje liniowe, ale o jakim równaniu, po prostu y?
6 sty 18:20
Szkolniak: Tak, w dwóch przypadkach wyjdzie ci po lewej stronie −y, wtedy mnożysz nierówność przez (−1)
6 sty 18:21
salamandra: założmy biorę 4−ty przypadek
y< 0 ⋀ x−1 < 0
−y ≤ −x+1 / * (−1)
y ≥ −x−1
i po prostu rozwiązaniem będzie to co "nad" prostą x−1?
6 sty 18:24
Saizou : Tak

6 sty 18:25
salamandra: Da się "niegraficznie" taki przedział określić?
6 sty 18:26
Saizou :
Da się, ale nic bardziej przejrzystego niż y≥−x−1 nie wymyślisz
Można to tak zapisać
A = {(x,y)∊R2: |y| ≤ |x−1|} ale to raczej za dużo ci nie mówi
6 sty 18:29
Szkolniak: Zadanie7
3√√5+2−3√√5−2=x, x>0
x=3√√5+2−3√√5−2 /3
x3=√5+2−33√(√5+2)2(√5−2)+33√(√5+2)(√5−2)2−√5+2
x3=4−33√√5+2+33√√5−2
x3=4−3(3√√5+2−3√√5−2)
x3=4−3x
x3+3x−4=0
x3−x+4x−4=0
x(x2−1)+4(x−1)=0
x(x+1)(x−1)+4(x−1)=0
(x−1)[x(x+1)+4]=0
(x−1)(x2+x+4)=0 /:(x2+x+4)
x−1=0, bo ⋀(x2+x+4>0)
x∊R
x=1∊C, cnw.
6 sty 18:36
a@b:
Zad.7
| | 1+√5 | | 1−√5 | |
( |
| )3= √5+2 , ( |
| )3=√5−2 |
| | 2 | | 2 | |
i mamy
6 sty 18:40
Saizou :
można tak, albo zauważyć wzór skróconego mnożenia
√5+2=.... kombinujcie

6 sty 18:40
a@b:

6 sty 18:43
Saizou :
Zostało 10 oraz 6 do zrobienia

6 sty 18:46
a@b:
zad10
Da się "zwinąć " ............
L=[k(k+1)(k+2)]
2 = 36u ,u∊N
i oczywiście
komentarz................

6 sty 18:50
Szkolniak: Zadanie 10
(k3+k2)(k2+3k+2)(k+2)=k2(k+1)(k+2)(k+1)(k+2)=k2(k+1)2(k+2)2=[k(k+1)(k+2)]2
są to trzy kolejne liczby naturalne, zatem są one na pewno podzielne przez 2 i przez 3,z czego
wynika, że na pewno są podzielne przez 6, a całość podniesiona jest do kwadratu, więc tym
samym wyrażenie jest podzielne przez 36, cnw.
6 sty 18:53
Saizou :
bardzo ładnie

6 sty 18:54
a@b:

dla
Szkolniak
6 sty 18:59
salamandra: zad 6.
|y| ≤ |x−1|
1) y ≥ 0 i x−1 ≥ 0
y≤ x−1 (rysuje prostą o równaniu x−1 i zaznaczam to co poniżej prostej)
2) y≥0 i x−1 < 0
y ≤ −x+1
(rysuje prostą o równaniu −x+1 i zaznaczam to co poniżej prostej)
3) y<0 i x−1 ≥ 0
−y ≤ x−1
y ≥ −x+1
(rysuje prostą o równaniu −x+1 i zaznaczam to co nad prostą)
4) y<0 i x−1 < 0
−y ≤ −x+1
y≥ x−1
(rysuje prostą o równaniu x−1 i zaznaczam to co nad prostą)
6 sty 19:05
Szkolniak:
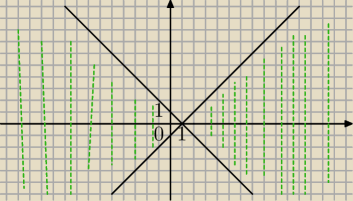
Lekko nabazgrane, jest okej?
6 sty 19:07
Saizou :
Jeszcze pytanie: czy proste należą do tego zbioru? Tak lub nie i dlaczego
6 sty 19:11
salamandra: W zadaniu 7 dwójka jest pod pierwiastkiem kwadratowym, czy tylko pod pierwiastkiem trzeciego
stopnia?
6 sty 19:11
salamandra: Należą, bo jest ≥ lub ≤
6 sty 19:12
Saizou :
pod pierwiastkiem 3 stopnia jest wyrażenie √5+/−2
i odpowiedź na pytanie: gratuluję, bardzo dobrze
6 sty 19:14
6 sty 19:32
Saizou :
Jest okej, tylko nazwij jeszcze po drodze co to jest w(c) i będzie bardzo poprawnie
6 sty 19:37
salamandra: zad 8.
x2+2x+x+2+y2+2y+y+2+1≥xy+2x+2y+4
x2−xy+y2+3x+2+3y+3 ≥ 2x+2y+4 / *2
2x2−2xy+2y2+6x+4+6y+6 ≥ 4x+4y+8
x2−2xy+y2+x2+y2+6x+4+6y+6≥ 4x+4xy+8
(x−y)2 + x2+6x+6 + y2+6y+4−4x−4y−8≥0
(x−y)2+x2+2x+6+y2+2y+4−8≥0
(x−y)2+(x+1)2+5+y2+2y+4−8≥0
(x−y)2+(x+1)2+5+y2+2y+4−8≥0
(x−y)2+(x+1)2+y2+2y+1 ≥ 0
(x−y)2+(x+1)2+(y+1)2 ≥ 0
suma trzech nieujemnych czynników będzie zawsze nieujemna, oraz wszystkie przekształcenia są
równoważne
c.n.u
6 sty 20:11
Saizou :
komentarz jest zły,
x−y∊R, ale (x−y)2≥0
x+1∊R, ale (x+1)2≥0
y+1∊R, ale (y+1)2≥0
==================+
(x−y)2+(x+1)2+(y+1)2 ≥ 0
komentarz: suma trzech wyrażeń nieujemnych jest nieujemna
6 sty 20:22
salamandra: 9b) nie bardzo wiem od czego zacząć,
9a)
|2x|+2 = 4
|2x| = 2
x = 1 v x = −1
6 sty 20:24
Saizou :
Zad 11
Wykazać, że dla każdego m∊N
+ liczba postaci
jest liczbą całkowitą
Zad 12
Wykaż, że liczba postaci
gdy n∊N jest kwadratem liczby naturalnej
Zad 13
Liczby naturalne dodatnie a, b, c, d spełniają warunek
3√abc=4 oraz
4√abcd=2
√10
oblicz wartość d
Zad 14
Liczbę sześciocyfrową utworzono przez zapisanie obok siebie dwa razy tej samej
liczby trzycyfrowej. Wykaż, że otrzymana w ten sposób liczba jest podzielna przez 13.
Zad 15
Wykaż, że każda liczba pierwsza większa od 3, jest postaci 6n+1 lub 6n+5, gdzie n∊N.
Zad 16
Wykaż, że jeżeli liczba naturalne n jest podzielna przez 3 i nie jest podzielna przez 6,
to liczba postaci n
2+7 jest podzielna przez 8
6 sty 20:34
a@b:
Zobacz wpis Szkolniaka 16:57
6 sty 20:35
salamandra: Nie wiem właśnie dlaczego pomnożył/podzielił przez |m| skoro |m| może być zerem? wnioskuję, że
stąd otrzymał |x|, a 1 przeniósł na drugą stronę
6 sty 20:36
a@b:
załóż,że m≠0
6 sty 20:37
a@b:
bo dla m=0 równanie sprzeczne
6 sty 20:38
salamandra: i dlatego założenie ≥ 0, bo |x| musi być ≥ 0?
6 sty 20:44
salamandra: |m|*|x|+|m| = 4
m≠0
|m|(|x|+1) = 4 / ( : |m| )
1) m≥0
(4−m)m≥ 0
(4−m)m = 0
m= 4 v m = 0
m∊(0; 4>, bo zero wyrzucone z dziedziny
2) m<0
(4+m)(−m)≥0
(4+m)(−m) = 0
m = −4 v m = 0
m∊ (−4;0)
suma: m∊ (−4;0) u (0;4>
6 sty 20:54
salamandra: W 11 podobna zabawa jak w 7, czy zupełnie inaczej trzeba zacząć?
6 sty 21:02
Saizou :
W 11 należy pokazać że licznik jest podzielny przez 12
6 sty 21:05
salamandra: Napisałeś, aby wykazać, że jest liczbą całkowitą
6 sty 21:07
Saizou :
20:54 jest dobrze
6 sty 21:07
Saizou : no tak, czyli musisz pokazać, że wyrażenie
(3m−5)(m3−3m2+2m)
jest podzielne przez 12
6 sty 21:08
Mila:
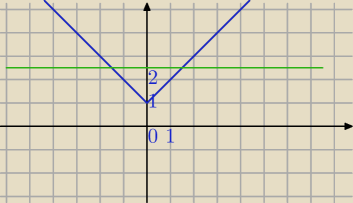
II sposób
|m|*(|x|+1)=4
1) m=0 to mamy: 0*(|x|+1)=4⇔0=4 sprzeczność ⇔brak rozwiązań
2)m≠0
g(x)=|x|+1
| | 4 | |
Równanie g(x)= |
| posiada rozwiązanie |
| | |m| | |
4≥|m|
m∊<−4,4>\{0}
6 sty 21:08
salamandra: A dlaczego akurat podzielne przez 12?
6 sty 21:14
Saizou :
bo chcesz pozbyć się mianownika
6 sty 21:16
salamandra: Nadal niestety nie rozumiem.
Ja to zacząłem tak, że znów wziąłem jakieś "c"
| | 3m−5 | |
i napisałem |
| (m3−3m2+2m) = c / *12 |
| | 12 | |
i w ten sposób się pozbyłem mianownika
6 sty 21:25
Saizou :
czyli masz równanie
12c=(3m−5)(m3−3m2+2m), gdzie c jest całkowite
czyli teraz musisz pokazać że prawa strona jest wielokrotnością liczby 12
6 sty 21:28
ite:
MEDAL DLA ZAŁOŻYCIELA TEGO WĄTKU
ZA POPULARYZACJĘ ZADAŃ MATURALNYCH
(w dni wolne od nauki szkolnej)
6 sty 21:28
ite: I za szybki rozwój wątku !
6 sty 21:29
Saizou :
@
ite dzięki, ale robię dokładnie to samo co
Eta kilka lat temu

6 sty 21:30
salamandra: jedyne co mi przyszło do głowy, to podstawić po m kolejne liczby naturalne i sprawdzić czy
będzie podzielne przez 12, ale nie tędy pewnie droga, bo dla m=1 i m=2, wychodzi 0,
6 sty 21:34
Saizou : Wszystkich licz i tak byś nie sprawdził

12=4*3 to jest podpowiedź
6 sty 21:40
salamandra: (3m−5)m(m2−3m+2) = 4*3*c ? coś takiego?
6 sty 21:44
Saizou : Nie, trzeba przedstawić lewa stronę w taki sposób, aby można z niej wywnioskować że jest ona
podzielna przez 3 i 4
6 sty 21:47
Eta:


6 sty 21:50
salamandra: Wymnożenie mi nic nie da w sumie, bo będę miał postać 3m4−14m3+21m2−10m, chyba, że tę postać
jakoś "zwinąć" inaczej?
6 sty 21:53
Saizou : Te postać jeszcze możesz rozłożyć
6 sty 21:54
salamandra: Mówisz o tej wyjściowej?
6 sty 21:58
salamandra: Jeśli tak, to wiem, że ten drugi nawias mogę przedstawić w postaci m(m−1)(m−2), bo
pierwiastkami tego drugiego nawiasu są: 0, 1 i 2
to miałbym (3m−5)m(m−1)(m−2), ale nadal mi to nic nie mówi
6 sty 22:04
Saizou :
3m−5=3m−9+4=3(m−3)+4
...= (3m−5)m(m−1)(m−2)=
[3(m−3)+4]m(m−1)(m−2)=
3(m−3)(m−2)(m−1)+4(m−2)(m−1)m
co możesz powiedzieć o każdym składniku tej sumy?
6 sty 22:16
Saizou : poprawka
3(m−3)(m−2)(m−1)m+4(m−2)(m−1)m
6 sty 22:16
Szkolniak: Zadanie 13
a,b,c,d∊N
+
3√abc=4 /
3
abc=64
4√abcd=2
√10 /
4
abcd=1600
d=25
6 sty 23:59
a@b:
14/
xyzxyz
100100x+10010y+1001z=1001(..........)
1001=7*11*13
7 sty 00:11
Szkolniak: Zadanie 12
| n4 | | n3 | | n2 | | n4+2n3+n2 | | n2(n+1)2 | | n(n+1) | |
| + |
| + |
| = |
| = |
| =( |
| )2 |
| 4 | | 2 | | 4 | | 4 | | 22 | | 2 | |
Potrzebny do tego komentarz o podzielności licznika przez 2 ze względu na dwie kolejne liczby
naturalne w liczniku?
7 sty 07:59
Saizou :
Zad 13 okej
Zad 12 komentarz jest potrzebny
Zad 14

7 sty 08:48
salamandra: 22:16, skąd się wzięło m+4, a na końcu jeszcze m?
7 sty 08:59
Saizou :
Rozbijasz czynnik
3m−5=3m−9+4=3(m−3)+4
I teraz mnożysz wyrażenia
...= (3m−5)m(m−1)(m−2)=
[ 3(m−3)+4]m(m−1)(m−2)
niebieskie * zielone + czerwone * zielone
7 sty 09:05
salamandra: to jak pomnoże 4 *m, to będę miał 4m, a nie 4+m?
7 sty 12:49
salamandra: poprosiłem o pomoc nauczyciela, powiedział żeby z postaci (do której ja doprowadziłem), czyli
(3m−5)m(m−1)(m−2) pokazać, że będzie liczba całkowita niezależnie od tego jakie m podstawie,
bo mnoże przez siebie 4 liczby całkowite
7 sty 12:50
Saizou :
Kolejność wykonywania działań, najpierw nawiasy, potem mnożenie.
Może Cię o mylić, bo zmieniłem kolejność czynników. Zapiszę to trochę inaczej
Mam nadzieję, że to rozbicie rozumiesz
3m−5=3m−9+4=3(m−3)+4
wówczas mamy
[3(m−3)+4]m(m−1)(m−2) =
3(m−3)m(m−1)(m−2)+4m(m−1)(m−2) porządkowałem to sobie, żeby mieć jakiś logiczny układ
=3m(m−1)(m−2)(m−3)+4m(m−1)(m−2)
3m(m−1)(m−2)(m−3)
Iloczyn 4 kolejnych liczb całkowitych jest podzielny przez 4 (3*4=12),
stąd podzielność pierwszego składnika przez 12
4m(m−1)(m−2)
iloczyn 3 kolejnych liczb całkowitych jest podzielny przez 3 (4*3=12),
stąd podzielność drugiego składnika przez 12
7 sty 13:07
salamandra: "3m(m−1)(m−2)(m−3)
Iloczyn 4 kolejnych liczb całkowitych jest podzielny przez 4 (3*4=12),
stąd podzielność pierwszego składnika przez 12 "
Czy rzeczywiście są to cztery kolejne liczby całkowite?
m= 2
6*1*0*(−1)
m= 3
9*2*1*0
m = 4
12*3*2*1?
7 sty 13:39
Saizou : dla m =2 masz
m→2
m−1→1
m−2→0
m−3→−1
dla m =3
m→3
m−1→2
m−2→1
m−3→0
dla m = 4
m→4
m−1→3
m−2→2
m−3→1
itd.
7 sty 13:43
salamandra: a 3m? co się dzieje z 3m?
7 sty 13:46
Saizou :
to jest rozbite 3*m(m−1)(m−2)(m−3)
wyrażenia traktujemy jako te 4 kolejne liczby całkowite (te na czerwono)
7 sty 13:48
salamandra: Aha, czyli z tego wniosek, że calosc będzie podzielna przez 12, i w drugim to samo tylko na
odwrót.
I czy to jest koniec zadania? Bo w zasadzie dlaczego trzeba uzasadniać podzielność przez 12?
Czy tu chodzi o to, żeby udowodnić że po podzieleniu przez 12 wynikiem będzie liczba całkowita
(bo dążę nie do 12c, tylko do c)?
7 sty 14:21
Saizou : Tak,
7 sty 14:54
Szkolniak: Odnośnie zadania 16−go:
Czy jest jakiś sposób żeby wpaść na to jak zapisać tę liczbę? Czy wiedza na temat tego jak
zapisywać liczby w takich zadaniach wynika po prostu z wyuczenia się 'na blachę'?
7 sty 18:00
salamandra: Ja jeszcze w zasadzie mam pytanie odnośnie tego "feralnego" 11−tego (dla mnie):
Skąd wynika, że iloczyn czterech kolejnych liczb naturalnych jest podzielny przez 4? da się to
udowodnić?
7 sty 18:10
ABC:
jedna z tych liczb dzieli się przez 4 skoro są kolejne

7 sty 18:13
Mila:
Podpowiedź:
1) Liczby naturalne podzielne przez możesz zapisać : 3k, k∊N wśród nich są podzielne przez 6.
2) Liczby podzielne przez 6 możesz zapisać tak: 6m, m∊N
Wszystkie są też podzielne przez 3, chodzi teraz o zapisanie liczby naturalnej tak, aby była
podzielna
przez 3 ale niepodzielna przez 6.
Wypisuję 6 pewnych kolejnych liczb w taki sposób:
6m, 6m+1, 6m+2,6m+3, 6m+4, 6m+5
Który zapis pasuje do Twojego zadania?
7 sty 18:15
Mila:
Mój komentarz dla Szkolniaka.
7 sty 18:17
salamandra: bo liczby podzielne przez 4 to 4n+4, gdzie n∊C?
7 sty 18:17
Szkolniak: Wnioskuję że ta liczba to 6m+3, zgadza się?
7 sty 18:25
a@b:
ok
7 sty 18:26
Szkolniak: Mogę dochodzić do postaci tych liczb podstawiajac sobie kolejno pod k czy m kolejne liczby
naturalne i patrzeć co się dzieje? Czy nie powinienem tak robić ze względu na to że nie jestem
w stanie sprawdzić co się dzieje ze wszystkimi takimi liczbami?
7 sty 18:27
salamandra: Jak rozgryźć 14?
Mało rozumiem z zapisu z 0:11 a@b
Ja to zacząłem tak
abcabc − sześciocyfrowa liczba, i to w sumie tyle
7 sty 19:04
a@b:
L=xyzxyz
L=100 000x+10 000y+1 000z+100x+10y+z
L=100100x+10010y+1001z= 1001(100x+10y+z) = 7*11*
13(100x+10y+z)
Czy teraz już jaśniej ?

7 sty 19:12
salamandra: A dlaczego 100 000x?
7 sty 19:15
a@b:
Jak zapiszesz liczbę np: 600 000 ? 6*..... ?
7 sty 19:18
salamandra: Czyli inaczej mówiąc jest to „rozbijanie” na części setek, jedności itp?
Podobna sekwencja jak w przypadku zamiany ułamka dziesiętnego na zwykły stosując szereg
geometryczny?
7 sty 19:20
a@b:
Liczba dwucyfrowa : 10x+y , gdzie, x∊{1,2,3,4,5,6,7,8,9,} , y∊{0,1,2,3,4,5,6,7,8,9}
liczba trzycyfrowa : 100x+10y+z
liczba sześciocyfrowa : 100 000x+10 000y+1 000z+100u+10w+v
7 sty 19:22
salamandra: Już pojąłem, dzięki

7 sty 19:28
a@b:

7 sty 19:29
salamandra: Tym bardziej natomiast nie rozumiem 15−tego. Jedyne co wiem o liczbach pierwszych, to, że
jedynymi dzielnikami jest 1 i owa liczba.
7 sty 19:31
a@b:
n>3 −− liczba pierwsza
n=6k −− ma więcej niż dwa dzielniki ( nie jest pierwsza
n=6k+1 −− może być pierwsza np dla k=1 n=7>3
n=6k+2 −− parzysta więc nie jest pierwszą >3
..............
dokończysz ?....
7 sty 19:39
Łukasz: Dla n=6k+5 też będzie nieparzysta a 6k+5 to jest to samo co n= 6k−1....
7 sty 19:47
salamandra: No te wzory są podane w zadaniu, ale nie wiem jak to wykazać, że
n = 6k+3 − nieparzysta, ma więcej dzielników niż dwa
n = 6k+4 − parzysta, więc nie jest pierwszą
n = 6k+5 i tak do 6k+9?
7 sty 20:18
Mila:
Nie do 9 , bo następna liczba jest podzielna przez 6, a ten przypadek już jest ujęty wcześniej.
7 sty 20:26
salamandra: która "następna"?
7 sty 20:50
Mila:
6k+6=6*(k+1) więc podzielna przez 6
7 sty 20:56
salamandra: znaczy, chciałem to zrobić w ten sposób, że pokazać właśnie, że 6k+6 − nie jest, 6k+7 − jest
(to to samo co 6k+1), 6k+8− nie jest, 6k+9− nie jest. Powyżej 10 to wiadomo, że będzie się
sekwencja powtarzać.
7 sty 21:02
Mila:
Saizou, piękne dałeś zadania, ale więcej tu nie pisz. Załóż nowy wątek.

7 sty 23:10
Saizou : Właśnie myślałem żeby założyć nowy wątek, jutro wrzucę coś z funkcji kwadratowej z parametrem i
wielomiany
7 sty 23:52
vnec: Zobacz sobie algorytm sita erastotenesa na liczby pierwsze, zaczynasz od 5 bo 2 i 3 sa
trywialne, potem masz 7 ( dodajesz 2) potem masz 11 ( dodajesz 4) i 13 ( dodajesz 2) i znowu
17 ( bo dodajesz 4 ) i tak dalej
8 sty 00:01








 .
pilnie tu na forum przygotowywali się do matury (z naszą pomocą )
bezpowrotnie minęły ! ( a szkoda
.
pilnie tu na forum przygotowywali się do matury (z naszą pomocą )
bezpowrotnie minęły ! ( a szkoda 
 Twoje rozumowanie w tym przykładzie jest słuszne
Twoje rozumowanie w tym przykładzie jest słuszne  źle przepisałem, miało być
źle przepisałem, miało być



 Szkolniak + komentarz o przekształceniach równoważnych i będzie super
Szkolniak + komentarz o przekształceniach równoważnych i będzie super

 Czyli (a−b)(a+b) = 3*5 ⇔ a−b = 3 ⋀ a+b = 5?
I potem brać inne pary? np. 5*3, 1*15, 15*1?
Czyli (a−b)(a+b) = 3*5 ⇔ a−b = 3 ⋀ a+b = 5?
I potem brać inne pary? np. 5*3, 1*15, 15*1?

 |mx|+|m|=4
ad a
m=2 ⇒ |2x|+2=4
2|x|=2
|x|=1
x=−1 v x=1
x∊{−1,1}
ad b
|mx|+|m|=4
|m|*|x|+|m|=4
|m|(|x|+1)=4
|mx|+|m|=4
ad a
m=2 ⇒ |2x|+2=4
2|x|=2
|x|=1
x=−1 v x=1
x∊{−1,1}
ad b
|mx|+|m|=4
|m|*|x|+|m|=4
|m|(|x|+1)=4

 w 1. przedziale x nie nalezy do dziedziny.
w 2 również, gdyż przedział otwarty.
więc x=0 to rozwiązanie., bo tylko w trzecim nalezy do przedziału.
w 1. przedziale x nie nalezy do dziedziny.
w 2 również, gdyż przedział otwarty.
więc x=0 to rozwiązanie., bo tylko w trzecim nalezy do przedziału.
 Warto pamiętać o takich rzeczach, żeby punkty na maturze nie leciały
Warto pamiętać o takich rzeczach, żeby punkty na maturze nie leciały


 8) x,y∊R ∧ x≠y
Przekształcam równoważnie daną nierówność:
(x+1)(x+2)+(y+1)(y+2)+1≥(x+2)(y+2)
x2+3x+2+y2+3y+2+1≥xy+2x+2y+4
x2+3x+y2+3y≥xy+2x+2y
x2+x+y2+y−xy≥0 /*2
2x2−2xy+2y2+2x+2y≥0
x2−2xy+y2+x2+2x+y2+2y≥0
(x−y)2+(x+1)2+(y+1)2≥2
x−y≥0
x+1≥1
y+1≥1
zatem suma ich kwadratów jest na pewno większa lub równa 2, cnw.
Jest okej?
8) x,y∊R ∧ x≠y
Przekształcam równoważnie daną nierówność:
(x+1)(x+2)+(y+1)(y+2)+1≥(x+2)(y+2)
x2+3x+2+y2+3y+2+1≥xy+2x+2y+4
x2+3x+y2+3y≥xy+2x+2y
x2+x+y2+y−xy≥0 /*2
2x2−2xy+2y2+2x+2y≥0
x2−2xy+y2+x2+2x+y2+2y≥0
(x−y)2+(x+1)2+(y+1)2≥2
x−y≥0
x+1≥1
y+1≥1
zatem suma ich kwadratów jest na pewno większa lub równa 2, cnw.
Jest okej?








 dla Szkolniak
dla Szkolniak
 Lekko nabazgrane, jest okej?
Lekko nabazgrane, jest okej?
 II sposób
|m|*(|x|+1)=4
1) m=0 to mamy: 0*(|x|+1)=4⇔0=4 sprzeczność ⇔brak rozwiązań
2)m≠0
II sposób
|m|*(|x|+1)=4
1) m=0 to mamy: 0*(|x|+1)=4⇔0=4 sprzeczność ⇔brak rozwiązań
2)m≠0
 MEDAL DLA ZAŁOŻYCIELA TEGO WĄTKU
ZA POPULARYZACJĘ ZADAŃ MATURALNYCH
(w dni wolne od nauki szkolnej)
MEDAL DLA ZAŁOŻYCIELA TEGO WĄTKU
ZA POPULARYZACJĘ ZADAŃ MATURALNYCH
(w dni wolne od nauki szkolnej)

 12=4*3 to jest podpowiedź
12=4*3 to jest podpowiedź







