Całka ograniczona krzywymi Nick: Witam. Mam takie zadanie: Oblicz całkę ∫∫(3x − siny) dxdy jeśli obszar D jest ograniczony krzywymi x=0, x= π/2, y=0, y − x = 0 Zrobiłem coś takiego: ∫^π/2₀ dx ∫^x₀ (3x − siny) dy = ∫^π/2₀ [cosy]^x₀ dx = ∫^π/2₀ cosx dx = [sinx]^π/2₀ = 1 Sprawdzałem to na kalkulatorze w internecie i wyniki się nie zgadzają, w kalkulatorze wychodzi coś takiego: ¹₈(8−4π+π³) Mógłby mi ktoś pomóc, gdzie zrobiłem błąd?

albi: źle policzyłeś całkę ∫(3x − siny)dy

Nick: cosx − cos0? o to chodzi?

albi: Nie, zastanów się czy całka z tego to na pewno sam cosinus

albi: A oprócz tego cosx − cos0 ≠ cosx

Nick: No to w takim razie chodzi o to 3x, tylko nie mam pojęcia co z nim zrobić, myślałem że to omijamy gdyż biorę pod uwagę to co przy y

albi: Nie, uznajesz 3x jako współczynnik, możesz go równe dobrze dać za znak całki

albi: Powinno być ∫(3x−siny)dy = 3x∫dy − ∫(siny)dy

Nick: y + cosy?

albi: Dokładniej to 3xy + cosy

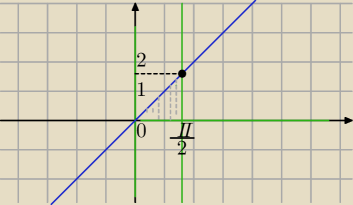
Mila: x=0, x= π/2, y=0, y − x = 0 ₀∫^π/2[₀∫^π/2(3x−siny)dy]dx=

	3π
=0∫π/2([3xy+cosy]0π/2)dx=0∫π/2[		x−1]dx=
	2

	3π		3π		π		π
=[		x2−x]0π/2=		*(		)2−		=
	4		4		2		2

	3π3		π
=		−
	16		2