Parametr Xxx: Dla jakich wartości parametru m równanie −x²+3x+|x−4|=m ma jedno rozwiązanie?

salamandra: a = −1 ≠ 0 x≥ 4 −x²+3x+x−4 = m −x²+4x−m−4 = 0 Δ = 0 (nie rozpatrujemy przypadku gdy a = 0, bo nie a = −1, nie stoi przy nim parametr m) Δ = 16 + 4(−m−4) =16−4m−16 = −4m Δ=0 ⇔ m = 0 x<4 −x²+3x−x+4 = m −x²+2x−m+4 = 0 Δ = 0 Δ=4+4(−m+4) = 4+−4m+16 = −4m+20 Δ = 0 ⇔ −4m+20 = 0 −4m+20 = 0 −4m = −20 / : (−4) m = 5

salamandra: Powinno być dobrze

ite: Musisz sprawdzić, czy dla wyliczonych wartości parametru, to jedyne rozwiązanie należy do rozpatrywanego przedziału.

salamandra: W pierwszym przypadku x=2, więc nie należy, a w drugim x = 1, czyli nalezy

ite: tak, jest tylko jedno rozwiązanie

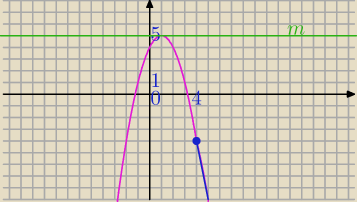
Mila: II sposób −x²+3x+|x−4|=m x≥4 f(x)=−x²+4x−4 x<4 f(x)=−x²+3x−x+4 f(x)=−x²+2x+4 f(x)=5 jedno rozwiązanie dla m=5 jedno rozwiązanie