trapez Kira: Pole trapezu równoramiennego opisanego na okręgu o promieniu r jest równe P. Wyznacz pole czworokąta, którego wierzchołkami są punkty styczności tego okręgu z trapezem. Podaj stosowne załozenia

a@b: Hej Mila działasz? ( bo nie chcę na darmo pisać dubla

a@b:

	8r4
Odp: S=
	P

===========

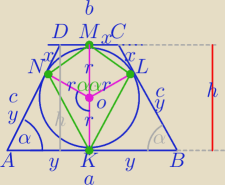
Mila: h=2r a+b=2c− okrąg wpisany trapez

	a+b
1)		*2r=P
	2

(a+b)*r=P 2cr=P

	P
c=
	2r

	h		2r		4r2
2) sinα=		=		⇔sinα=
	c		P   2r		P

AKON− deltoid i promienie są prostopadłe do boków trapezu, zatem z sumy katów czworokąta: α+|∡NOK|=180^o

	1
PΔNOK=PKOL=		*r2*sin(180−α)=
	2

	1		1		4r2
=		r2*sinα=		*r2*
	2		2		P

	2r4
PΔNOK=
	P

3) suma kątów przy ramieniu tr. jest równa 180^o |∡MOL|=|∡MON=α|

	2r4
PΔMOL=		=PΔNOM
	P

4)

	2r4		8r4
PKLMN=4*		=
	P		P

=========================

a@b:

	√P
i jeszcze założenie r∊(0,		>
	2

	√P
dla r=		trapez jest kwadratem o boku 2r
	2

Mila: