Geometria Basia: W sześcianie ABCDA'B'C'D' o krawędzi długości 150 punkt P jest środkiem krawędzi AA', punkt Q środkiem krawędzi BC, zaś punkt R, środkiem przekątnej górnej podstawy. Oblicz cos kąta PQR

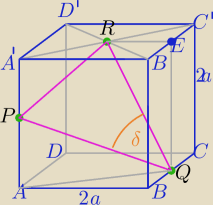
Mila: 2a=150 1) W ΔPA'R: |PR|²=a²+(a√2)² ⇔|PR|²=3a² W ΔABQ: |AQ|²=(2a)²+a² ⇔|AQ|²=5a² W ΔPAQ: |PQ|²=a²+5a² ⇔|PQ|²=6a² 2) |QR|=|AQ| W ΔREQ: |RQ|²=5a2 3) W ΔPQR: z tw. cosinusów |PR|²=|PQ|²+|RQ|²−2*|PQ|*|RQ| *cosδ 3a2=6a²+5a²−2*a√6*a √5 cosδ /:a² 3=6+5−2√30 cosδ 8=2√30cos δ

	4		2√30
cosδ=		=
	√30		15

==============

Basia: a jeszcze jak obliczyć pole powierzchni trójkąta PQR

Mila: δ− kąt ostry

	2√30
sin2δ=1− (		)2
	15

	7
sin2δ=
	15

	√7
sinδ=
	√15

	1
PΔPQR=		*|PQ|*|QR|*sinδ
	2

dokończ Masz odpowiedź do zadania?

Basia: no właśnie nie mam

Mila: To dokończ i napisz wynik.