W sześcianie ABCDA'B'C'D'... . Oblicz cos kąta PQR i pole powierzchni trójkąta P rodo: W sześcianie ABCDA'B'C'D' o krawędzi długości 30 punkt P jest środkiem krawędzi AA', punkt Q środkiem krawędzi BC, zaś punkt R środkiem przekątnej górnej podstawy. Oblicz cos kąta PQR i pole powierzchni trójkąta PQR.

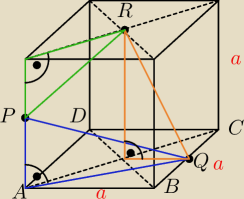
Szkolniak: (górne oznaczenia wierzchołków pominąłem, w takiej samej kolejności wpisywane) a=30 b=PQ d=AQ g=RQ f=PR d²=30²+15² d²=1125 ⇒ d=15√5 b²=d²+15² (trójkąt niebieski) b²=1350 ⇒ b=15√6

	a
g2=(		)2+a2 (trójkąt pomarańczowy)
	2

g²=1125 ⇒ g=15√5

	a		a√2
f2=(		)2+(		)2 (trójkąt zielony)
	2		2

f²=225+450 f²=675 ⇒ f=15√3 niech α=∡PQR z twierdzenia cosinusów: f²=g²+b²−2*g*b*cosα 675=1125+1350−450√30*cosα −1800=−450√30*cosα

	1800		2√30
cosα=		⇒ cosα=
	450√30		15

pole próbowałem policzyć z Herona, ale nie wiem czy jest to najoptymalniejszy sposób tutaj, może ktoś inny wpadnie na szybszy sposób

Mila: α− kąt ostry

	4*30
sin2α=1−
	225

	7
sin2α=
	15

	√7
sinα=
	√15

	1
PΔPQR=		|PQ|*|QR|*sinα
	2

	1		√7
PΔPQR=		*15√6*15√5*
	2		√15

dokończ