 Witam. Mam do obliczenia taką całkę iterowaną i narysować obszar całkowania
∫dy∫√y2+1dx D : 0 ≥ y ≥ √8
0 ≥ x ≥ y
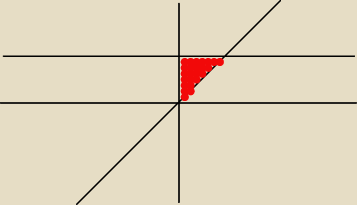
Na wykresie powyżej zaznaczyłem ten obszar, wydaje mi się że jest prawidłowy. Ale mam
ważniejsze pytanie, nie mogę znaleźć sposobu na rozwiązanie tego pod pierwiastkiem.
gdzieś przeczytałem, że powinienem zrobić coś mniej więcej takiego:
y2 + 1 = t / ddy , wychodzi nam, że dy = dt2y
Potem to podstawiamy ale wychodzą mi głupoty, więc nie wiem czy do końca to jest dobry pomysł
Witam. Mam do obliczenia taką całkę iterowaną i narysować obszar całkowania
∫dy∫√y2+1dx D : 0 ≥ y ≥ √8
0 ≥ x ≥ y
Na wykresie powyżej zaznaczyłem ten obszar, wydaje mi się że jest prawidłowy. Ale mam
ważniejsze pytanie, nie mogę znaleźć sposobu na rozwiązanie tego pod pierwiastkiem.
gdzieś przeczytałem, że powinienem zrobić coś mniej więcej takiego:
y2 + 1 = t / ddy , wychodzi nam, że dy = dt2y
Potem to podstawiamy ale wychodzą mi głupoty, więc nie wiem czy do końca to jest dobry pomysł
| 1 | 1 | 26 | ||||
=∫0a y √y2+1 dy = | [(y2+1)3/2]0a= | (27−1)= | ||||
| 3 | 3 | 3 |