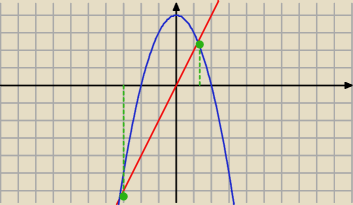
objętość przy obrocie wokół osi OX w potrzebie: Oblicz objętość bryły powstałej przez obrót wokół osi x obszaru ograniczonego krzywym y = −x² + 4, y = 2x

Blee: no to licz odpowiednią całkę

w potrzebie: czyli jaką?− pls napisz mi tylko całkę

Blee: π∫_x1^x₂ [(−x²+4)² − (2x)²] dx

w potrzebie: thx

Leszek: Najpierw wyznacz punkt przeciecia : y =2x , y = −x² +4 ⇒ x= √5 −1 Nastepnie V= π [ ∫ 4x² dx + ∫ (−x² + 4)² dx ]= .... Pierwsza calka w granicach od 0 do √5 −1 , druga od √5 − 1 do 2 Zrob rysunek to wszystko zobaczysz !

Blee: Leszek ... dlaczego dodajesz

Leszek: Nie zrobilem rysunku , sorry , kolega @Blee pokazal dobrze ! x₁ i x₂ otrzymujemy z rozwiazania rownania : 2x = −x² + 4

w potrzebie: Taaa, to już zrozumiałe