Ekstremum Lancelot: Jak to zrobić ? Znajdź ekstremum lokalne funkcji : |x² −5x+6| proszeee o pomoc

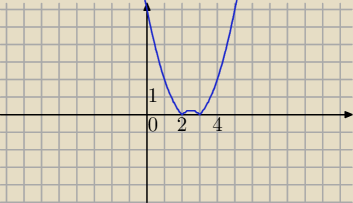
Mila: f(x)=|x²−5x+6| 1) |x²−5x+6|≥0 Ekstrema dla x=2 lub x=3 minima lokalne : f(2)=f(3)=0

	5		5		1
lub dla xw=		mamy maksimum lokalne: ymax=|f(		| =
	2		2		4

Lancelot: A z pochodną jak to będzie ?

Lancelot: Proszę o jakikolwiek pomysł

jc: Pochodna nie wskaże ekstremów w punktach 2 i 3 bo w tych punktach funkcja nie jest różniczkowalna.

Lancelot: Ale chyba da się wyznaczyć ekstrema ? Granice trzeba policzyć?

Blee: 1) Jesteś spostrzegawczy i widzisz, że f(x) = |x²−5x+6| to nic innego jak parabola z naniesioną wartością bezwzględną, więc masz dwie opcje: a) jest jedno ekstremum i jest to wierzchołek paraboli (x_wierzchołka i y_wierzchołka) i jest to minimum lokalne −−− ponieważ wartość bezwzględna nic nie zmienia w postaci funkcji, b) masz trzy ekstrema: x_wierzchołka (ale −y_wierzchołka) i jest to maksimum oraz dwa minima w punktach w których wartość wyrażenia w module = 0 Nie trzeba żadnych pochodnych ... wystarczy trochę ruszyć głową

Lancelot: Dobrze a z takim przykładem jak sobie poradzić: x²|x−1| i wyliczyć ekstrema

ite:

	⎧	x2(x − 1) gdy x≥1
f(x) =	⎨
	⎩	−x2(x − 1) gdy x<1

Z pomocą pochodnej sprawdzasz istnienie ekstremów w przedziałach (−∞,1) i (1,∞). Dla x=1 pochodna nie istnieje, więc zawsze trzeba sprawdzić, czy funkcja nie ma w tym punkcie ekstremum.

Lancelot: Ite, proszę powiedz jak mam sprawdzić to istnienie w tych przedziałach i dla punktu x=1

ite: Oblicz pochodną funkcji x²(x − 1), przyrównaj do zera i sprawdź, czy punkt podejrzany o ekstremum należy do (1,∞). Jeśli tak, to czy pochodna zmienia w nim znak. Funkcja f(x)=x²|x−1| również będzie mieć tam ekstremum. Tak samo z funkcją −x²(x − 1), ale sprawdzanie czy należy do przedziału (−∞,1). Dla x=1 sprawdzamy na podstawie definicji ekstremum lokalnego.

Lancelot: A jak na podstawie definicji to zrobić?

Lancelot: I jak mam ustalić czy jest to max czy min ?

Mila: f(1)=0 lim_x→1−f(x)=0 lim_x→1+f(x)=0⇔f(x) jest funkcją ciągłą f(x)≥0 dla x∊R zatem w x=1 ma minimum.

Lancelot: A na tych przedziałach jak ustalić jakie to ekstremum ?

Jerzy: A na których przedziałach ?

ite: 1/ dla x∊<1,∞) f(x)=x²(x − 1)=x³−x², jest różniczkowalna w przedziale (1,∞)

	2
f '(x)=3x2−2x=3x(x−		)
	3

Szukam miejsc zerowych f.pochodnej

	2		2
3x(x−		)=0 → x=0 ∨ x=
	3		3

Sprawdzam, czy punkt podejrzany o ekstremum należy do (1,∞)

	2
0∉(1,∞),		∉(1,∞)
	3

Funkcja nie ma w przedziale (1,∞) ekstremów. 2/ dla x∊(−∞,1) f(x)=−x²(x − 1)=−x³+x², jest różniczkowalna na tym przedziale

	2
f '(x)=−3x2+2x=−3x(x−		)
	3

Szukam miejsc zerowych f.pochodnej

	2		2
−3x(x−		)=0 → x=0 ∨ x=
	3		3

Sprawdzam, czy punkt podejrzany o ekstremum należy do (1,∞)

	2
0∊(−∞,1),		∊(−∞,1), warunek konieczny jest spełniony.
	3

Teraz pozostaje sprawdzić warunek dostateczny (zmiany znaku f.pochodnej).

Mila: cd Myślałam, że to już rozwiązałeś. x<1 f(x)=x²*(−x+1)=−x³+x² f'(x)=−3x²+2x f'(x)≥0⇔x*(−3x+2)≥0

	2
⇔x∊<0,		>
	3

w x=0 ma minimum ,bo pochodna zmienia znak przy przejściu przez x=0 z (−) na (+) ( tak skrótowo to zapisałam, chyba rozumiesz?)

	2		2
a w x=		ma maksimum bo pochodna zmienia znak przy przejściu przez x=		z (+) na
	3		3

(−)

Mila: Przepraszam ite, nie widziałam Twojego wpisu.

ite: Milu mam potwierdzenie, że dobrze liczę

Lancelot: Dziękuję wszystkim!