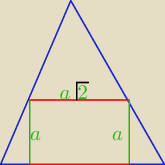
Stożek, sześcian.
kcmJ:
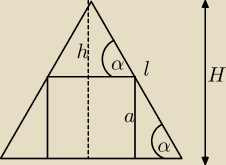
Tworząca stożka ma długość l i jest nachylona do płaszczyzny podstawy pod kątem a(alfa). W
stożek ten wpisano sześcian tak, że cztery jego wierzchołki należą do powierzchni bocznej
stożka, zaś 4 pozostałe należą do podstawy stożka. Znajdź długość krawędzi sześcianu.
Rozw.:
sinα = H/l => H = l sinα
tgα = h / 0,5a => h = 0,5a tgα
H = a + h
H= a + 0,5tgα = a(1 + tgα/2)
l sinα = a(1+tgα/2) => a= (2lsinα) / (2+ tgα)
W odpowiedzi jest: a= (2lsinα) / (2+
√2tgα), różnica
√2 i znam rozwiązanie poprawne z
podobieństwa trójkątów, ciekawi mnie jednak co w moim rozumowaniu jest złe, że wyszedł
nieprawidłowy wynik? H nie dzieli a na połowę?
kcmJ: Juz wiem.
Jeśli sobie wyobrazimy tą figurę, to sześcian w stożku styka się z jego powierzchnią
wierzchołkiem, a nie krawędzią, zatem to co widzimy na przekroju podstawy mniejszego trójkąta,
to przekątna, zatem d=a
√2, a dokładnie 0,5d.
