trygonometria
Nikto0: Witam. Proszę o pomoc.

w funkcji sinx+|sinx| do jakiego przedziału należą x−iksy Mam wykres
tylko nie umiem tego odczytać
31 gru 12:00
Jerzy:
Dziedziną funkcji f(x) = sinx + |sinx| jest R.
Dla sinx ≥ 0 , f(x) = 2sinx
Dla sinx < 0 , f(x) = 0
31 gru 12:18
Jerzy:
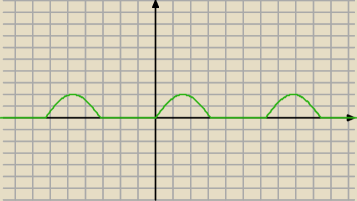
31 gru 12:20
Nikto0: A jak wyrazić okresowość tej funkcji?
31 gru 12:56
Jerzy:
Taki sam jak okres funkcji f(x) = sinx
31 gru 12:58
Nikto0: Bo mam zapisane x należy od −pi+2kpi;0+2kpi nie wiem czy zamknięty przedział czy otwarty
x należy <0+2kpi

i+2kpi> ale nie rozumiem dlaczego?
31 gru 13:12
Nikto0: zamiast minki <0+2kpi ; pi+2kpi>
31 gru 13:12
Jerzy:
Nie wypisuj głupot, tylko napisz pełną treść zadania.
31 gru 13:13
Nikto0: W treści mam narysuj wykres funkcji i nie wiem właśnie dlaczego coś takiego znalazło się w
moich notatkach
Myślałam że to jest jakiś okres funkcji dodatkowo napisany do tego zadania.
31 gru 13:22
Jerzy:
Patrz 12:18
Dla: sinx ≥ 0 , czyli dla: x ∊ <0 + 2kπ,π + 2kπ> , f(x) = 2 sinx
Dla pozostałych x , f(x) = 0
31 gru 13:26
Nikto0: Ale jak skorzystam z π + 2kπ i za k podstawię 1 to wyjdzie 3π a tam jest f(x)=0
31 gru 14:16
Jerzy:
No i tak ma być.
31 gru 14:25
Nikto0: Czyli π + 2kπ jest dla sinx=0?
31 gru 14:29
Jerzy:
Dla dowolnej wielokrotności π sin(kπ) = 0
31 gru 14:31
Nikto0: To jest tak jak pisałam?
31 gru 14:37
Nikto0: w takim razie nie wiem skąd jest π + 2kπ
31 gru 14:39
Jerzy:
Jak opiszesz wszystkie przedziały, w których sinx > 0 ?
31 gru 14:45
Nikto0: od 0+2kπ
31 gru 14:47
Nikto0: A w tym przedziale <0 + 2kπ,π + 2kπ> nie są zawarte wartości po ujemnej stronie układu
współrzędnych dlaczego?
31 gru 14:55
Jerzy:
Czy ty nie czujesz ,że 14:55 to jest nieskończenie wiele przedziałów, a nie jeden ?
W tych przedziałach funkcja sinx jest nieujemna.
31 gru 15:03
Nikto0: czyli k może być ujemne?
31 gru 15:11
Jerzy:
Tak, k to liczba całkowita.
31 gru 15:13
Nikto0: Ale dalej nie wiem skąd jest π + 2kπ?
31 gru 15:15
Jerzy:
Podstawowym przedziałem jest <0,π> i teraz dla opisania wszystkich przedziałów dodajemy okres
zasadniczy 2kπ i mamy <0 + 2kπ,π + 2kπ>
31 gru 15:19
Nikto0: A moje stwierdzenie Czyli π + 2kπ jest dla sinx=0? z 14:29 jest poprawne?
31 gru 15:22
Nikto0: Nie rozumiem tego

31 gru 15:23
Jerzy:
Jeśli sinx = 0, to x = kπ, czyli sin(π + 2nπ) = 0 , gdzie n to liczna całkowita.
31 gru 15:26
Nikto0: Czyli to jest poprawne?
31 gru 15:31
Nikto0: Nie wiem dlaczego π + 2kπ jest w tym przedziale jak to jest równe zeru
31 gru 15:32
Jerzy:
π + 2kπ , to argument i nigdy nie jest równy 0, przyjmuje wielokrotności π,
dla k = 0 mamy π,dla k = 1 mamy 3π,dla k = 2 mamy 5π,itd....
31 gru 15:50
Nikto0: A dlaczego np.jest 3π kiedy tam wykres nie jest powyżej zera?
31 gru 15:54
Jerzy:
sin(kπ) = 0,a więc sin(3π) =0
31 gru 16:01
Nikto0: A czym to się różni π + 2kπ od pozostałych f(x)=0
31 gru 16:14
Jerzy:
Widziałaś na oczy wykres funkcji sinx ? Popatrz to zobaczysz,że posiada miejsca zerowe w
wielokrotnościach π , np: − 5π, 145π, −2357π
31 gru 16:18
Nikto0: Ale poza wielokrotnościami π też wartość y=0
31 gru 16:23
Jerzy:
Nie, bo wtedy byłaby to funkcja stała: y = 0
31 gru 16:29
Nikto0: A te miejsca z którymi pokrywa się oś x to nie to samo co miejsca zerowe w wielokrotnościach
pi?
31 gru 16:33
Jerzy:
Tam gdzie wykres przecina oś OX,tam są miejsca zerowe (to niematematyczne,ale może dotrze do
ciebie)
31 gru 16:41
Nikto0: Dziękuję.

1 sty 09:49
Nikto0: Mam pytanie Czy dla f(x)=0 x należy (π+2kπ;0+2kπ) i dlaczego od π a nie od −π?
7 sty 16:02
Nikto0: Ktoś może odpowiedzieć na pytanie

7 sty 19:59
Mila:
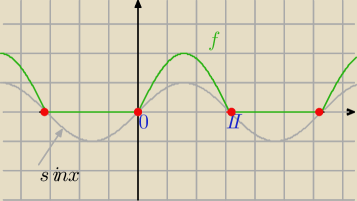
f(x)=sinx+|sinx|
|sinx|=sinx jeżeli sinx≥0⇔0+2kπ≤x≤π+2kπ przy czym sin(0)=0 , sin(π)=0
wtedy:
f(x)=2sinx i f(0)=0 , f(π)=0
|sinx|=−sinx jeżeli sinx<0 ⇔ π+2kπ<x<2π+2kπ wtedy:
f(x)=0 bo sinx−sinx=0
f(x)=0 jeżeli π+2kπ≤x≤2π+2kπ
Jeżeli podstawisz k=−1 to będziesz miała przedział:
<−π, 0>
7 sty 20:23
Nikto0: Nie rozumiem

7 sty 20:30
Mila:
Czego nie rozumiesz?
Pytasz dla jakich argumentów f(x)=0.
Narysowałam wykres y=sin(x), abyś widziała, kiedy sinx≥0 w pozostałych przedziałach sinx<0
f(x)= 0 tam gdzie sinx=0 i tam gdzie sinx<0.
f(x)=0 dla x∊<π+2kπ,2π+2kπ >
ale możesz też zapisać:
f(x)=0 dla x∊<−π+2kπ, 0+2kπ>
f(x) jest funkcją okresową.
7 sty 20:37
Nikto0:
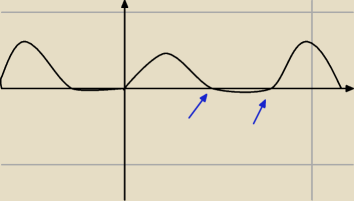
Nie rozumiem jak to wyznacza dlaczego jest to przedział od π kiedy to zaczynają się miejsca
zerowe a w 2π zaczynają się wartości dodatnie
Według mojego rozumowania powinny się w obu przypadkach zaczynać tam gdzie są miejsca zerowe
nie rozumiem tego
8 sty 11:01
Mila:
Miejsca zerowe funkcji y=sinx zaznaczone na czerwono.
8 sty 17:33
 w funkcji sinx+|sinx| do jakiego przedziału należą x−iksy Mam wykres
tylko nie umiem tego odczytać
w funkcji sinx+|sinx| do jakiego przedziału należą x−iksy Mam wykres
tylko nie umiem tego odczytać

 i+2kpi> ale nie rozumiem dlaczego?
i+2kpi> ale nie rozumiem dlaczego?



 f(x)=sinx+|sinx|
|sinx|=sinx jeżeli sinx≥0⇔0+2kπ≤x≤π+2kπ przy czym sin(0)=0 , sin(π)=0
wtedy:
f(x)=2sinx i f(0)=0 , f(π)=0
|sinx|=−sinx jeżeli sinx<0 ⇔ π+2kπ<x<2π+2kπ wtedy:
f(x)=0 bo sinx−sinx=0
f(x)=0 jeżeli π+2kπ≤x≤2π+2kπ
Jeżeli podstawisz k=−1 to będziesz miała przedział:
<−π, 0>
f(x)=sinx+|sinx|
|sinx|=sinx jeżeli sinx≥0⇔0+2kπ≤x≤π+2kπ przy czym sin(0)=0 , sin(π)=0
wtedy:
f(x)=2sinx i f(0)=0 , f(π)=0
|sinx|=−sinx jeżeli sinx<0 ⇔ π+2kπ<x<2π+2kπ wtedy:
f(x)=0 bo sinx−sinx=0
f(x)=0 jeżeli π+2kπ≤x≤2π+2kπ
Jeżeli podstawisz k=−1 to będziesz miała przedział:
<−π, 0>

 Nie rozumiem jak to wyznacza dlaczego jest to przedział od π kiedy to zaczynają się miejsca
zerowe a w 2π zaczynają się wartości dodatnie
Według mojego rozumowania powinny się w obu przypadkach zaczynać tam gdzie są miejsca zerowe
nie rozumiem tego
Nie rozumiem jak to wyznacza dlaczego jest to przedział od π kiedy to zaczynają się miejsca
zerowe a w 2π zaczynają się wartości dodatnie
Według mojego rozumowania powinny się w obu przypadkach zaczynać tam gdzie są miejsca zerowe
nie rozumiem tego