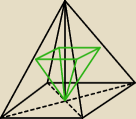
 W ostrosłup prawidłowy ABCDS o podstawie kwadratowej został wpisany ostrosłup prawidłowy EFGHS1
tak, że S1 jest spodkiem wysokości ostrosłupa ABCDSa wierzchołki kwadratu EFGH należą do
odpowiednich krawędzi bocznych AS, BS, CS, DS (patrz rysunek). Jaką częścią objętości
ostrosłupa ABCDS jest największa objętość ostrosłupa EFGHS1?
W ostrosłup prawidłowy ABCDS o podstawie kwadratowej został wpisany ostrosłup prawidłowy EFGHS1
tak, że S1 jest spodkiem wysokości ostrosłupa ABCDSa wierzchołki kwadratu EFGH należą do
odpowiednich krawędzi bocznych AS, BS, CS, DS (patrz rysunek). Jaką częścią objętości
ostrosłupa ABCDS jest największa objętość ostrosłupa EFGHS1?
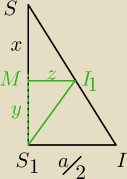 zauważ, że:
0) robimy przekrój równoległy do boku podstawy
1) ΔSMI1 jest podobny do ΔSS1I
2) hostrosłupa głównego = x+y
3) a, h sto stałe (wartości głównego strosłupa)
4) y = h − x
zauważ, że:
0) robimy przekrój równoległy do boku podstawy
1) ΔSMI1 jest podobny do ΔSS1I
2) hostrosłupa głównego = x+y
3) a, h sto stałe (wartości głównego strosłupa)
4) y = h − x
| z | a/2 | ax | ||||
5) z tw. podobieństwa trójkątów: | = | −> z = | ||||
| x | h | 2h |
| 1 | 4 | ax | ||||
Vostrosłupa małego = | (2z)2*y = | ( | )2*(h−x) | |||
| 3 | 3 | 2h |
 !
!