Najwieksze i najmniejsze wartości Nick: Witam. Mam takie zadanie: Znajdź największe i najmniejsze wartości funkcji f(x,y) = x{2) + y² − 6y na zbiorze x² + y² ≤ 3. Więc tak, obliczyłem pierwsze pochodne f'x i f'y. Z tego mi wyszedł punkt (0,3), który się nie znajduje na tym zbiorze, czyli wykluczam. Potem szukalem ekstremum na brzegach i wyszła mi sprzeczność: x = √3−y², y ∊ <−√3,√3> Rozważmy funkcję h(y) h(y) = f(√3−y², y) h'(y)= −6 h'(y) = 0 ⇔ −6 ≠ 0 − sprzeczność No i wychodzi na to że nie ma żadnej wartości największej i najmniejszej. Czy coś pominąłem lub źle obliczyłem?

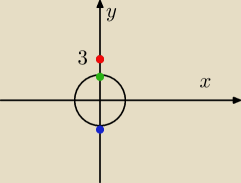
jc: f=x²+y²−6y ? f=x²+(y−3)²−9 x²+y² ≤ 3 f to nieco pomniejszony kwadrat odległości od czerwonej kropki. Interesuje nas wartość f na kole. Minimum mamy w u góry koła − punkt (0,√3), maksimum u dołu − punkt (0,−√3).

xyz: https://www.wolframalpha.com/input/?i=max+and+min+value+of+f%28x%2Cy%29+%3D+x%5E2+%2B+y%5E2+-+6y+where+x%5E2+%2B+y%5E2+%3C%3D+3

Nick: No dobra, chyba wszystko rozumiem, w sumie to co napisałem chyba nie jest złe. Mam jeszcze jedno pytanko. Czy przy tym: h'(y)= −6 h'(y) = 0 ⇔ −6 ≠ 0 − sprzeczność Mógłbym dodać komentarz że funkcja jest liniowa i osiąga ekstrema(czy coś w tym stylu)? No bo w sumie to się zgadza...