Ciekawe zadanka Jack: Ta sekcja będzie odpowiadać za ciekawe (wg mnie xd) zadanka. Zadanie nr 1. Monika umieściła monetę oznaczoną literą "P" w kwadracie znajdującym się na środku planszy 7x7. Na ile sposobów może ona ułożyć słowo "Pies" poprzez przemieszczenie się do 3 innych kwadratów, jeżeli może się ona poruszać jedynie do sąsiadujących kwadratów (pionowo, poziomo, skos) (Patrz rysunek)

Blee: 1) a₁ = 8*5*7 a₂ = 8*2*5 a₁ + a₂ = 8*5*9

Jack: hmm, tu mam napisane, że odp. to 104

Maciess: 4*3*3+4*4*3+4*1*5

Jack: Jakby co wszystkie zadanka sa z poziomu podstawowki/gimnazjum. Zadanie 2. Jaka jest reszta z dzielenia liczby 2018²⁰¹⁸ przez 20 ?

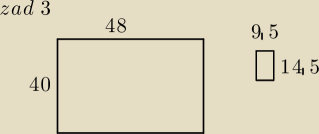
Jack: Zadanie 3. Mamy pudełko o wymiarach 40 x 48. Ile prostokątnych smartfonów do niego wejdzie, jeżeli rozmiar smartfona wynosi 9,5 x 14,5 Chodzi tylko o zapełnienie dna (zatem głębokość się nie liczy) (Patrz rys)

Adamm: Zd 3. 29+19 = 48, więc myślę, że 13

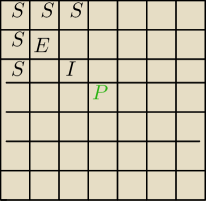
a7: 4*3*3=4*9=36 przypadków gdy idziemy do litery i umieszczonej na górze, na dole na lewo lub na prawo (czyli4 razy 3, gyż każda ztych liter e może iść do trzech liter e następnie każda z liter e może iść do trzech liter s. 4*4*3+4*5=48+20=68 przypadków gdy idziemy do litery i po skosie (takich skosów mamy cztery (patrz rysunek), następnie jeśli idziemy do litery e po skosie w lewo do góry to mamy 5 liter s dlatego 4*1*5 lub idziemy do litery E np. w prawo lub w prawo dól po skosie lub w górę lub w górę lewo po skosie (cztery takie możliwości) i wtedy możemy iść do trzech liter s dlatego 4*4*3) 68+36=104

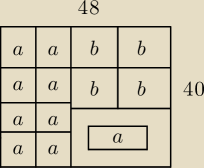
Adamm: a oznacza, że strona 9,5 jest równoległa do 40, b, że równoległa do 48 możemy włożyć 13 telefonów jak na rysunku, ale 14*9,5*14,5 > 40*48 więc już nie możemy włożyć ich 14

Jack: 13 to poprawna odpowiedź. Ktoś coś zadanie 2? Zadanie 4. Istnieją dwie takie liczby całkowite n,

	12−√n
dla których wyrażenie		daje liczbę całkowitą.
	4−√7

Ile wynosi suma tych liczb?

janek191: Jedną z tych liczb jest 63.

Jack: zgadza się.

Jack: ta druga jest prostsza. a w międzyczasie Zadanie 5. Niech a, b będą dodatnimi liczbami rzeczywistymi,

	1
takimi, że a +		= 7.
	b

	1
Jaką najmniejszą wartość da wyrażenie b +
	a

ite: 4/ n=144

Mila: 4) n= 63 lub n=144

Adamm: 4. wyniki zostały podane, tylko skąd je wziąć, nie zgadując?

12−√n		(12−√n)(4+√7)
	=
4−√7		9

teraz, by (12−√n)(4+√7) było wymierne, to √n musi być postaci a+b√7, czyli = √7k lub = k dla pewnej liczby całkowitej nieujemnej k (bez uzasadnienia)

	(12−√7k)(4+√7)		48−7k		12−4k
zatem		=		+√7*
	9		9		9

skąd k = 3 i n = 7*9 = 63 lub k = 12 i n = 144

Mila: Przekształcałam , tak jak Ty

Adamm: c = 1/b a+c = 7

2		a+c
	≤
1   1   + a   c		2

⇒

	1		1		1
4/7≤		+		=		+b
	a		c		a

równość gdy a = c = 3,5

ite: Ja też nie zgadywałam, a janek191 to już napewno policzył.

Adamm: zapomniałem, to było zd 5 jeśli chodzi o zd 2, nie chce mi się tego robić bez kongruencji, nie widzę sensu

ite: *na pewno

Adamm: Rozwiązałem dosyć dużo zadań (bo aż 3!), więc wstawiam swoje zadanie. Jako, że to nie Jack wstawia, to daję prim temu zadaniu, żeby odróżnić od tych, które wstawia Jack. Zadanie 1' Wskaż wszystkie dodatnie całkowite liczby n, takie, że kwadrat można podzielić na n kwadratów.

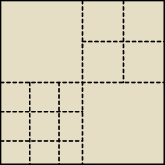
ite: Chodzi o np. taki podział ?

Adamm: tak

Mila: Bez kongruencji: Reszta z dzielenia 2018²⁰¹⁸ przez 20 . 2018²⁰¹⁸=(2020−2)²⁰¹⁸=20k+2²⁰¹⁸, k∊C Kolejne reszty z dzielenia potęg liczby 2 przez 20 2,4,8,16||,12,4,8,16,||12,4,8,16,||12,4,8,12... 2²⁰¹⁸=2²⁰¹⁶*2²=(2⁴)⁵⁰⁴*4=4*(20m+16)⁵⁰⁴=4*(20n+16)=40n+64= =40n+3*20+4, dla m,n∊N ⇔2018²⁰¹⁸ =20k+40n+3*20+4=20s+4 , gdzie s∊N

Jack: Oczywiście inni też mogą wrzucać tu ciekawe zadania, to nie monopol Zadanie 6. Niech P(n) będzie liczbą przekątnych w n−kącie foremnym. Jeżeli P(a) + P(b) = 125 to ile wynosi a + b ?

Jack: Zadanie 7. Jakub, Leon, Izak, Grześ, Piotr i Robert mają usiąść przy okrągłym stole. Leon chce siedzieć koło Jakuba, a Izak nie chce siedzieć kogo Grzesia. Jeżeli miejsca przy stole są nierozróżnialne to na ile sposobów można wszystkich rozsadzić?

ite: 6/ a + b = 25

Jack: zgadza się, a skąd ten wynik?

Jack: Zadanie 8. Pierwszym elementem ciągu o dodatnich liczbach całkowitych jest liczba dwucyfrowa. Jeżeli N reprezentuje element ciągu, to następny element ciągu wynosi: ◯ 2*N jeżeli N < 100 ◯ 2*N − 100 jeżeli 2*N ≥ 100 Jeżeli 7 element ciągu wynosi 68, to ile wynosi 5 element tego ciągu?

ite: 8. Czy pierwszy warunek ma być taki: 2*N jeżeli 2*N < 100 ? Jeśli tak, to piąty element ciągu to 92, tak ?

Jack: tak, pardon, powinno być 2*N < 100. 92 to poprawna odp.

Jack: Zadanie 9. Liczby całkowite x i y wybierane są losowo, w taki sposób, że: −5 ≤ x ≤ 5 oraz −5 ≤ y ≤ 5 Jakie jest prawdopodobieństwo następującego zdarzenia: (x+y)² > x² + y²

Adamm: zd9 Niech A to zdarzenie, że: (x+y)² > x²+y² ⇔ xy>0 Niech B to zdarzenie, że: xy ≠ 0 ⇔ x ≠ 0 oraz y ≠ 0

	1		1		102
P(A) =		*P(B) =		*
	2		2		112

Jack: zgadza się.

student: no to dawaj kolejne zadanie

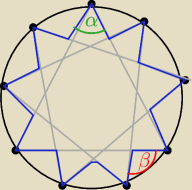
Jack: Widzę 7−dmego nikt nie chce : D Zadanie 10. (To na szaro potrzebowałem do narysowania gwiazdy proszę się nie sugerować) Mamy gwiazdę 9 ramienną (patrz rys.) Wartość kąta alfa wynosi 56 stopni i jest identyczna w każdym z rogów (pardon za rysunek na którym tego tak nie widać, ale w każdym z tych wierzchołków jest ten sam kąt) Ile wynosi kąt beta?

Des: Zad 10. 101 ?

Des: *106

ite: 360^o−(2*70^o+2*62^o)=96^o

Jack: Odp. do zad 10 to 96 stopni

ite:

Maciess: Zad 7 144?

Adamm: Zadanie 7. J, L, I, G, P i R mają usiąść przy okrągłym stole. L chce siedzieć koło J, a I nie chce siedzieć koło G. Jeżeli miejsca przy stole są nierozróżnialne to na ile sposobów można wszystkich rozsadzić? usadźmy najpierw L i J. Możemy to zrobić na 2 sposoby Reszta może być usadzona na 4!−2!*3! = 12 spososbów Razem = 12*2 = 24 sposoby

Jack: Tutaj odpowiedzi do ponizszych zadan 11 − 1 12 − 984 13 − 2178 14 − 45 15 − √15 16 − 40 17 − 2

Jack: Jako, że już nie będę miał tyle czasu to wrzucam teraz trochę więcej... Zadanie 11 Maciej poszedł na imprezę z 10 znajomymi i rozmawiał z każdą możliwą parą znajomych. W każdym przypadku co najmniej jedna osoba z pary z którą rozmawiał lubiła psy. Jeżeli Maciej lubi psy to jaka największa liczba osób na imprezie nie lubi psów? Zadanie 12 Niech zarówno N jak i 4N reprezentują liczby trzycyfrowe. Jeżeli suma cyfr liczby N wynosi 12, to jaką największą liczbą jest 4N ? Zadanie 13 Pomiędzy 1968 a 1982 rekord świata w biegu na 100 metrów zmalał z 10,03 sekundy do 10,00 sekund. Jeżeli rekord malałby liniowo (w ten sam sposób) to w którym roku zostałby osiągnięty rekord Usaina Bolta (z 2009r.) 9,58 sekundy Zadanie 14 Niech p będzie prawdopodobieństwem, że w 10 rzutach uczciwą monetą nigdy nie trafimy reszki. Niech q będzie prawdopodobieństwem, że w 10 rzutach uczciwą monetą trafimy reszkę dokładnie 2 razy.

	q
Ile wynosi iloraz		?
	p

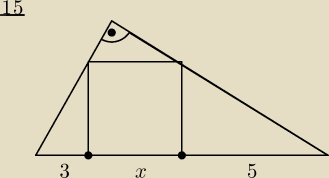
Zadanie 15 Kwadrat jest wpisany w trójkąt (patrz rys.). Jeżeli wierzchołki kwadratu dzielą przeciwprostokątną na odcinki 3,x,5, to ile wynosi x ? Zadanie 16 Niech odwróceniem 3−cyfrowej liczby ABC będzie liczba CBA dla cyfr A, B i C. Ile istnieje nieparzystych liczb 3−cyfrowych takich, że ABC − CBA = 198 ? Zadanie 17 Jan dzieli iloczyn liczb nieparzystych 1 * 3 * 5 * ... * (n−2) * n przez iloczyn liczb parzystych 2 * 4 * 6 * ... * (n−1) * (n+1) i wyraża go jako ułamek właściwy R. Jeżeli n = 17, jaki jest największy czynnik pierwszy mianownika R?

Jack: @Adamm, zgadza się, 24

Adamm: zd17 A = 1 * 3 * 5 * ... * (n−2) * n B = 2 * 4 * 6 * ... * (n−1) * (n+1) 7 dzieli B raz, ale 7|A 5 dzieli B raz, ale 5|A 3 dzieli B 2*3*3 więc dzieli B 3 razy. Ale 3 dzieli A też trzy razy. Więc to musi być 2, jako że 2|B, ale 2 nie dzieli A

ite: 12/ z,y,x ∊ ℕ ∧ z,y,x ≤9 ∧ x≠0 z+y+x=12 N=x*100+y*10+z ∧ 100≤N≤999 4N=x*400+y*40+z*4 ∧ 100≤4N≤999 ⇒ x=1 ∨ x=2 skoro 4N ma być możliwie największą liczbą ⇒ x=2 wtedy x*400=800 i z+y=10 y*40+z*4≤999−800=199 ⇒ y<5 więc y=4 ⇒ z=10−4=6 4N=2*400+4*40+6*4=984

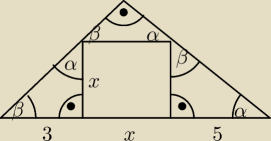
Szkolniak: x>0

	x
tgβ=
	3

	5
tgβ=
	x

x		5
	=		⇔ x2=15, więc x=√15, bo x>0
3		x

Szkolniak: Zadanie16) z=100a+10b+c, gdzie a∊{1,2,..,9} ∧ b∊{0,1,2,...,9} ∧ c∊{1,3,5,7,9} ABC−CBA=100a+10b+c−100c−10b−a=99a−99c 99a−99c=198 a−c=2 1) a=3 i b=0 i c=1 − jedna opcja + 9 kolejnych różnych wariantów z b (razem 10 opcji) 2) a=5 i b=0 i c=3 − jedna opcja + 9 kolejnych różnych wariantów z b (razem 10 opcji) 3) a=7 i b=0 i c=5 − | | − 4) a=9 i b=0 i c=7 − | | − Sumując otrzymujemy 40. Prosiłbym o sprawdzenie czy rozwiązanie jest logiczne dla drugiej osoby