Trójkąt - wykaż Marek: Witam, prosiłbym o pomoc z tym zadaniem: W trójkącie prostokątnym ABC o kącie prostym przy wierzchołku C poprowadzono środkowe z wierzchołków A i B , które przecięły się w punkcie D . Wykaż, że pole trójkąta ABD stanowi 1/3 pola trójkąta ABC .

Saizou : Jakiś własny pomysł?

Marek: Niech przyprostokątne mają długość 2a i 2b, a punkty E i F będą punktami, w których środkowe stykają się z bokami. Wtedy z trójkątów ACE i BCF można obliczyć długości tych środkowych. Wiedząc, że środkowe przecinają się w stosunku 2:1 to boki trójkąta ABD mają długość 2/3 |AE|, 2/3 |BF| i 4a²+4b² i potem można z Herona tylko wychodzą jakieś nieprzyjemne pierwiastki i ogólnie wydaję mi się, że można to zadanie rozwiązać łatwiej.

Marek: Tam powinno być √4a²+4b²

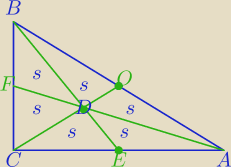
:.: : P_ΔABC=6s P_ΔABD=2s

2s		1
	=
6s		3

	1
PABD=		PABC
	3

:.: : Środkowe trójkąta dzielą go na 6 części o równych polach.

Marek: Troszkę nie widzę tego, że te 6 trójkątów maję równe pole, ale to już sam przeanalizuję. Dziękuję bardzo za pomoc!

:.: : https://matematykaszkolna.pl/forum/40418.html