trygonometria Nikto0: Witam. Proszę o pomoc. Dlaczego zadania 565 z linku nie mogę rozwiązać tak −1≤cos² alfa ≤1 /+1 https://zapodaj.net/ecc6844d0f967.jpg.html Drugie pytanie skąd w zadaniu 567 z linku drugiego wyrażenie pod pierwiastkiem treść zadania 567 https://zapodaj.net/f83ce68585aac.jpg.html rozwiązanie 567 https://zapodaj.net/808414b494a39.jpg.html

ite: 565/ −1≤cos α≤1 → 0≤cos²α≤1

Nikto0: Co zrobiłeś z postacią wyjściową −1≤cos α≤1 ?

Nikto0: Znaczy się z tym −1≤cos2 alfa ≤1

ite: 567/ wykorzystano wzór na cosinus podwojonego kąta

	α		α
cos α=cos(2*		)=1−sin2*(		)
	2		2

ite: 565/ Kwadrat dowolnej liczby rzeczywistej jest nieujemny. Czy widzisz wykorzystanie tej własności w przejściu −1≤cos α≤1 → 0≤cos²α≤1

Nikto0: nie widzę tego ani wykorzystania wzoru na cosinus podwójnego kąta A to nie miał sinus w 567

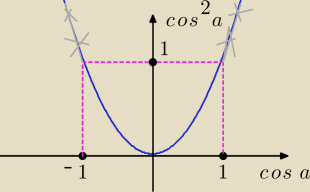
ite: Jeżeli wartość (cos α) należy do przedziału <−1,1>, to (cos²α) przyjmuje wartości z przedziału <0,1>. Tę sytuację ilustruje granatowy fragment wykresu funkcji kwadratowej.

Nikto0: A jak to podnieść do kwadratu <−1,1> mi podniesione do kwadratu wychodzi <1,1>

ite: 567/ W tablicach maturalnych jest podany wzór cos(2α)=1−sin²(α). W zadaniu 567/ jest podany cos(α). Trzeba ten wzór przekształcić, żeby móc go wykorzystać.

	α
Zauważam, że cos(α)=cos(2*		) i we wzorze z pierwszej linijki wszędzie
	2

	α
w miejsce α wstawiam		. Otrzymuję
	2

	α		α
cos(2*		)=1−sin2(		).
	2		2

565/ Jak z wykresu odczytujesz wartości cos²(α), to otrzymujesz przedział <1,1> czy <0,1> ? To jest zadanie typu "jaką najmniejszą wartość przyjmuje funkcja kwadratowa w przedziale ...". Podniesienie nierówności −1≤cos α≤1 stronami do kwadratu, to nie jest prawidłowy sposób rozwiązywania.

Nikto0:

	alfa
567. Zamiast 1−sin2		nie powinno być coś z cosinusem bo w odpowiedziach pod
	2

pierwiastkiem jest cosinus? Jak dojść do postaci w której będzie cosinus? 565. To jaki jest prawidłowy sposób?

ite:

	α
567/ Po podstawieniach z 12:51 otrzymujesz wzór cos(α)=1−sin2(		).
	2

	α
Teraz wylicz z niego sin(		).
	2

565/ Masz funkcję kwadratową i podany przedział, najmniejszej wartości szukaj, korzystając z wykresu z 12:32..

Nikto0: 567 rozumiem 565 Ale skąd mam wiedzieć jakie wartości przyjmuje cos²alfa?

ite: Wykres funkcji f(x)=x² znasz. Teraz potrzebujesz wykres f(cos α)=(cos α)²=cos²α. Skoro (cos α) przyjmuje tylko wartości z przedziału <−1,1>, to z wykresu funkcji kwadratowej odczytujesz wartości funkcji dla argumentów z tego właśnie przedziału. Widać, że funkcja przyjmuje wtedy wartości z przedziału <0,1>. Zapisujesz cos²α∊<0,1> albo w postaci nierówności 0≤cos²α≤1 .

Nikto0: Dalej nie rozumiem zadania 565

ite: 12:02 napisałaś −1≤cos²α≤1. Dla jakiego kąta α zachodzi równość −1=cos²α ?

Nikto0: nie wiem

Jerzy: Czy kwadrat dowolnej liczby może być ujemny ?

Nikto0: nie może być

Nikto0: ujemny

Jerzy: Dlatego cos²x ∊ <0,1>

Nikto0: Ale skąd się bierze w tym przedziale 0 i 1?

Nikto0: Jerzy już rozumiem. Dziękuję

Nikto0: A w 567 można inaczej rozwiązać korzystając z sinusa podwojonego kąta?

ite:

	α
cos(α)=1−sin2(		)
	2

↑ ↑ podany szukasz

	α		α
sin(α)=2*cos(		)*sin(		)
	2		2

↑ ↑ ↑ nieznany nieznany szukasz

Nikto0: Czyli się nie da?

ite: Da się, ale dużo liczenia: najpierw wyliczyć sin(α) z jedynki trygonometrycznej,

	α		α
potem cos(		) przedstawić za pomocą sin(		) (więc równanie kwadratowe po drodze).
	2		2

I to niepotrzebnego liczenia, a tylko ludzie leniwi tworzą postęp (podobno).

Nikto0: Jak liczę z jedynki trygonometrycznej to pod pierwiastkiem mam 1−cos² czy to miałabym Uprościć potem to wyrażenie z jedynki trygonometrycznej mam podstawić pod sinalfa/2?

ite: Dlaczego próbujesz liczyć tym drugim, dziwacznym sposobem, zamiast wykorzystać podaną w treści wartość cos α ? ? ? Nie można tak zapisać 1−cos² (!) , więc nie wiadomo, o co chodzi w tym pytaniu.

Nikto0: miało być 1−cos²alfa

ite: Jeśli chcesz obliczyć sin α, to musisz skorzystać z tego wzoru i z podanych w zadaniu wartości cos α i ćwiartki do której kąt α należy.

mam pytanie: 567 wzór cos2α=1−2sin²α α jest kątem ostrym więc sin alfa większy od zera (pierwsza ćwiartka same plusy)

	α
więc cosα=1−2sin2
	2

	α
2/3=1−2sin2
	2

1/6=sin²α

	1		√6
sinα=√		=
	6		6

Nikto0: A w 565 mam brać pod uwagę jakąś część funkcji cosinus czy całość i dlaczego?

Jerzy: Wykorzystaj: cos²x = 1 − sin²x

Jerzy: f(x) = 3 − 2sin²x f_min = 3 − 2 = 1

Nikto0: Skąd wziąłeś f(x) = 3 − 2sin²x fmin = 3 − 2 = 1

Jerzy: Patrz 11:21

Nikto0:

	α
A jak z tego wyliczyć sinα 1−cosα=sin2(		)
	2

Nikto0:

	α
przepraszam miało być jak wyliczyć sin
	2

Nikto0:

	1−cosα
Skąd w odpowiedziach pojawia się √		Skąd jest ta dwójka?
	2

Jerzy: 12:16 z prawej ma być: 2sin²(α/2)

Nikto0: Dziękuję.