 Bardzo proszę o pomoc jak rozwiązać to zadanie?
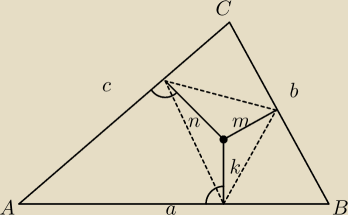
Z punktu S wewnątrz trójkąta ostrokątnego
opuszczono na boki a, b i c odcinki prostopadłe
− odpowiednio k, m i n.
Oblicz stosunek pola trójkąta do
pola trójkąta o wierzchołkach w rzutach punktu S na boki.
Bardzo proszę o pomoc jak rozwiązać to zadanie?
Z punktu S wewnątrz trójkąta ostrokątnego
opuszczono na boki a, b i c odcinki prostopadłe
− odpowiednio k, m i n.
Oblicz stosunek pola trójkąta do
pola trójkąta o wierzchołkach w rzutach punktu S na boki.
| abc | ||
odpowiedź: | ||
| amn+bnk+cmk |
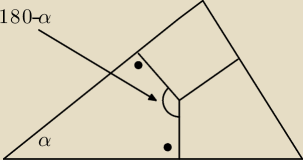 PΔABC=1/2(ak+bm+cn) PΔABC=1/2acsinα więc sinα=...... PΔnk=1/2nksin(180−α)=1/2nksinα
PΔABC=1/2(ak+bm+cn) PΔABC=1/2acsinα więc sinα=...... PΔnk=1/2nksin(180−α)=1/2nksinα
| ak+bm+an | ||
więc PΔnk=1/2nk* | ||
| ac |
| ak+bm+an | ||
PΔnk=1/2nk | ||
| ac |
| ak+bm+an | ||
PΔmk=1/2mk | ||
| ab |
| ak+bm+an | ||
PΔmn=1/2mn | ||
| bc |
| PΔABC | |
= | |
| PΔnk+PΔmk+PΔmn |
| nk(ak+bm+an) | mk(ak+bm+an) | mn(ak+bm+an) | ||||
[1/2(ak+bm+an)] : [1/2 | +1/2 | +1/2 | ]= | |||
| ac | ab | bc |
| abc | ||
=......= | ||
| amn+bkn+ckm |