stożek mat20: W stożek wpisano kulę Wykaż,że zachodzi równość Vk/Vst= P_c.k/P_c.st

Eta:

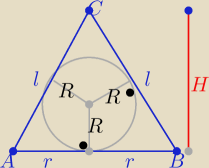
	2r+2l
Pole ΔABC: P=Rp, p=		⇒p=r+l
	2

P=R(r+l) i P=rH

	rH		r2H2
to R=		R2=
	r+l		(r+l)2

Vk		4r3H3		4rH2
	=.......=		=
Vst		r2H(r+l)3		(r+l)3

=======

Pk		4R2		4rH2
	=		= ....=
Pst		r(r+l)		(r+l)3

========

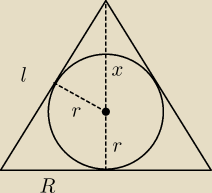Blee: Zrobiłeś rysunek Rysunek przekroju? zaznaczyłeś cokolwiek na nim? Wypisałeś wzory na pola całkowite i objętości 1) x = H − r 2) z podobieństwa trójkątów:

r		R		Rx
	=		−> r =
x		l		l

	Vk		r3		R3x3		Rx3
3)		= 4		= 4		= 4
	Vst		R2H		l3R2H		l3H

	Pck		r2		R2x2		Rx2
4)		= 4		= 4		= 4
	Pcst		R(R+l)		l2R(R+l)		l2(R+l)

5*)

r		R
	=		⇔ xR = l*r ⇔ xR + x*l = l*x + l*r ⇔ xR + x*l = l*H ⇔
x		l

	x		1		Rx3		Rx2
⇔		=		⇔ 4		= 4
	l*H		R+l		l3H		l2(R+l)

c.n.w.

Eta: