Zbiory liczb zespolonych na płaszczyźnie. Sheriff: Korzystając m.in. z interpretacji geometrycznej modułu liczby zespolonej opisać i zaznaczyć na płaszczyźnie zespolonej następujące zbiory spełniające poniższe warunki (a) 0<Re(iz)<1 (b) −1<Im(z+5)<1 (c) Re(^z−2_z−1)=0 Proszę o rozwiązanie powyższych przykładów. To są jedyne przykłady które nie wiem jak ugryźć ani na wykładzie ani na ćwiczeniach takich nie robiliśmy a na kolokwium wszystko może się zdarzyć.

Blee: mówisz że to są jedyne których nie umiesz no to na początek powiedz czemu jest równe: Re(z) Im(z)

Sheriff: Jeśli założymy że z=x+yi gdzie x i y ∊ R to Re(z) = x, a Im(z) = y

Blee: więc Re(iz) = Re(i(x+iy)) = Re(ix −y) = −y ... prawda Natomiast Im(z + 5) =

Sheriff: Im(z+5)=Im(x+iy+5)=Im(x+5+iy)=y Jeśli chodzi o (c) Im(^z−2_z−1)=Im(^x−2+iy_x−1+iy) | teraz usuwam i z mianownika mnożąc licznik i mianownik przez (x−1−iy) i wychodzi mi| Im[(u(x²−3x+2+y²+iy)/(x²+2x+1+y²) ale czy coś mi to da?

Sheriff: W tym ostatni Im nie powinno być 'u', zapomniałem usunać

Blee:

z−2		z−1		1		1
	=		−		= 1 −		<−−− trochę łatwiejsza postać, nie
z−1		z−1		z−1		z−1

sądzisz

Blee:

1		1		1		(x−1) − iy
	=		=		*		=
z−1		(x−1) + iy		(x−1) + iy		(x−1) − iy

	(x−1) − iy
=
	(x−1)2 + y2

więc

	z−2		(x−1) − iy
Im(		) = Im(1 −		) = ...
	z−1		(x−1)2 + y2

Blee: to na koniec narysuj bądź napisz co to będą za zbiory (wszystkie trzy podpunkty)

Sheriff: Prawda wygląda łatwiej ale nie widzę co mogę z tym zrobić. Podstawianie za z wydaję się prowadzić donikąd ale może się mylę

Sheriff: Wiadomośc napisałem przed odświeżeniem strony

Blee:

z−2		1		(x−1) − iy
	= 1 −		= 1 −		=
z−1		z−1		(x−1)2 + y2

	x−1		y
= 1 −		+ i−
	(x−1)2 + y2		(x−1)2 + y2

więc co tutaj jest częścią urojoną Dodatkowo pytanie −−− jak inaczej można zapisać (x−1)² + y² (chodzi o zapis przy użyciu 'z' )

Blee: 21:24 ... bez tego '−' po i a przed ostatnim ułamkiem

Sheriff: Nie wiem czy dobrze myślę ale w c to chyba Im=y/(x−1)² + y²

Blee: dokładnie (tylko nawias ma być )

	y
więc masz:		= 0 <−−−− i rysujesz/piszesz 'co to jest'
	(x−1)2 + y2

tak samo pozostałe podpunkty −−− narysuj/napisz co to za zbiory są i nie zapomnij o odpowiedzi na 'bonusowe pytanie' z 21:24

Sheriff: (x−1)²+y² = |z₀| gdzie z₀ = (x−1)+iy ?

Sheriff: 21:32 tam powinno być|z₀|²

Blee: 21:35 <−−− si senior no to jeszcze dajesz te zbiory (najprościej narysować) i po sprawie

Blee: 21:35 więc de facto można było to zapisać jako:

	z−2		1		(z−1)*
Im(		) = Im (1 −		) = Im( 1 −		)
	z−1		z−1		|z−1|2

gdzie (z−1)* oznacza sprzężenie liczby z−1

Sheriff: (a)0<Re(iz)≤1 Re(iz)=−y ⇒ −y≤1 i −y>0 ⇒ y≥−1 i y≤0 (b)−1<Im(z+5)<1 Im(z+5)=y ⇒ y<1 i y>−1 (c) Re(^z−2_z−1)=0 Re=1−[(x−1)/((x+1)²)+y²)] ⇒ x−1 = 0 ⇒ x=1 Tego (c) nie jestem pewien

Sheriff: 21:48 (c) −x+1=0 x=−1

Blee: a) czyli jaki zbiór rysunek (łatwiej) bądź napisać b) to samo pytanie

	z−2		(x−1)
c) Re(		) = 0 ⇔ 1 −		= 0 ⇔ (x−1)2 + y2 = (x−1)
	z−1		(x−1)2 + y2

Blee: wskazuje, jakie przekształcenie musisz jeszcze zrobić: (x−1)² − (x−1) = x² − 2x +1 − x + 1 = x² − 3x + 2 = x² − 2*1.5x + 2.25 − 0.25 = (x − 3/2)² − 1/4 i w efekcie co otrzymasz w (c)

Blee: Idę zapalić ... więc na spokojnie pokombinuj ... jak wrócę to sprawdzę i ewentualnie podpowiem

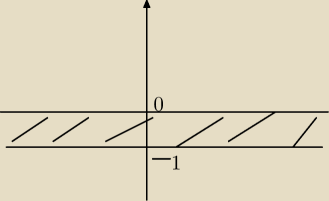
Sheriff: to jest wykres do (a) w (b) będzie od −1 do 1 z ich wyłaczeniem a (c) to okrąg o S(1,0) i prosta y=x−1? Wybacz że nie rysuję ale nie mam za bardzo czasu

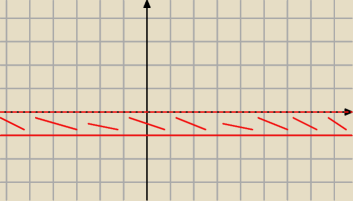
Blee: a) o ile to jest 0 < Re(iz) ≤ 1

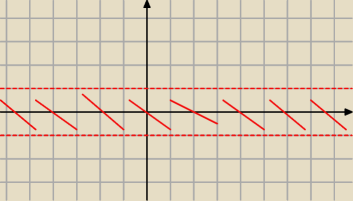
Blee: b) (jeżeli nierówności są 'słabe' )

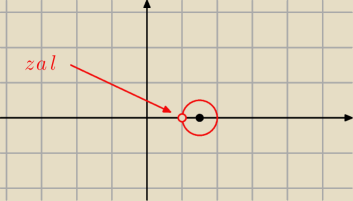
Blee: c) zał. z−1 ≠ 0 ⇔ z ≠ 1 ⇔ x ≠ 1 tutaj przecież wyszło: (x−1)² + y² = (x−1) co później Ci pokazałem że można zapisać jako: (x − 3/2)² + y² − 1/4 = 0 czyli: (x − 3/2)² + y² = 1/4 czyli: (x − 3/2)² + y² = (1/2)²

Sheriff: 22:15 faktycznie nie pomyślałem aby 1/4 zmienić (1/2)². Dziękuje Blee że pomogłeś mi to zrozumieć. Jeśli zaliczę kolokwium to będzie też dzięki tobie