Funkcja wymierna Dream: Podaj wzór funkcje homograficzne g której wykres przecina oś oy w punkcie a i ma ten sam środek symetrii co wykres funkcji f Naszkicuj wykres funkcji g F(x)= 3x+6/2−x A(0,−2)

ite: Dopóki nie użyjesz nawiasów, nie będziesz mieć funkcji homograficznej.

janek191:

	3 x + 6
Czy f(x) =		?
	2 − x

Dream: Tak

Mila:

	3x+6		3x−6++12		3*(x−2)+12
f(x)=−		=−		=−		⇔
	x−2		x−2		x−2

	12
f(x)=−3−
	x−2

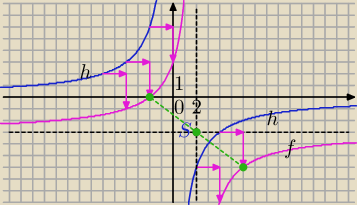
Mila: 1) Środek symetrii funkcji homograficznej

	3x+6
f(x)=
	2−x

	−12
f(x)=−3+		wykres tej funkcji powstaje z wykresu funkcji:
	x−2

	−12
h(x)=		przez przesunięcie o wektor [2,−3]
	x

S=(2,−3)− środek symetrii f(x)

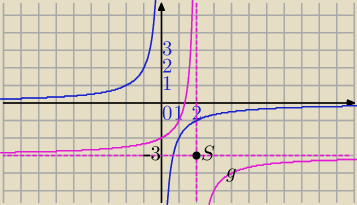
Mila: 2) A=(0,−2)

	k
g(x)=		+q − kanoniczna postać szukanej funkcji
	x−p

S=(p,q)=(2,−3)− środek symetrii wykresu

	k
g(x)=		−3
	x−2

g(0)=−2

k
	−3=−2
0−2

k
	=1⇔k=−2
−2

	−2
g(x)=		−3
	x−2

a )

	−2
Rysuję wykres y=		i przesuwam o wektor [2,−3]
	x

b) otrzymuję wykres g(x)

Blee: Mila ... nie sądzisz że trochę przekombinowane

	3x+6
f(x) =
	2−x

I. przecięcie się asymptot wyznacza środek symetrii funkcji homograficznej II. jedna z asymptot uczeń od razu winien potrafić określić −−− jest nią x = 2 III. drugą −−− to już zależy od poziomu 'zaawansowania' powiedzmy że nie umie od razu zauważyć, więc robimy przekształcenie:

	3x+6		3x+6		(3x − 6) + 12		12
f(x) =		= −		= −		= −3 −
	2−x		x−2		x−2		x−2

i z tej postaci odczytujemy, że drugą asymptotą jest y = −3 IV. skoro środek symetrii ma być zachowany to czerwona i niebieska część ma pozostać bez zmian

	b
g(x) = a +
	x − c

	b
więc g(x) = −3 +
	x−2

V. podstawiamy współrzędne punktu:

	b
−2 = −3 +		−> b = −2
	−2

VI. więc

	2
g(x) = −3 −
	x−2