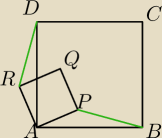
planimetria salamandra: Czworokąty ABCD i APQR są kwadratami. Wykaż, że BP = DR Mógłbym prosić o wskazówkę? W książce jest, że niby miara kąta RAD = PAB, ale nie wiem skąd to wiadomo, skoro ten kwadrat APQR nie jest przechylony o 45 stopni

ICSP: ∡RAD + ∡DAP = 90^p = ∡DAP + ∡PAB

ICSP: to p to jest o. Bądź niewrażliwy/a na zmianę literek.

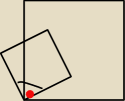
salamandra: Stąd to wynika? Tak z góry też spytam − jak wy robicie tak dokładne rysunki tu na forum? Ja bynajmniej nie potrafię, nie mam też zbyt wielu opcji, żeby zrobić dokładny wykres lub rysunek, bardzo mnie te opcje ograniczają.

ICSP: Wynika to z tego, ze są to kwadraty, więc ich kąty przy wierzchołkach mają miarę 90^o. Co do rysunków pytaj Ety lub Mili.

salamandra: 1) RAD+DAP = 90 2) PAB + DAP = 90 RAD+DAP = PAB+DAP RAD = PAB Boki przy tym kącie są równe, więc podobieństwo na zasadzie BKB?

salamandra: Jak mam dwa boki równe i kąt między nimi zawarty równy, to trzeci bok w obu trójkątach musi być taki sam?

ICSP: nie podobieństwo a przystawanie. To coś mocniejszego. Podobieństwo mówi, że możesz jeden dopasować do drugiego rozszerzając bądź zwężając boki ( oczywiście odpowiednio) Przystawanie mówi, że trójkąty są identyczne.

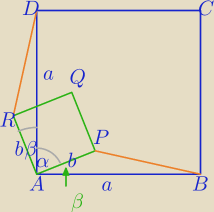
Mila: α+β=90^o α+|∠PAB|=90^o⇔|∠PAB|=β ΔABP≡ΔADR cecha bkb

salamandra: Powtórzę pytanie, czy jak dwa boki są równe i kat miedzy nimi zawarty to mam stuprocentowa pewność ze trójkąty są przystające?

Mila: Poznaj cechy przystawania trójkątów: bbb,bkb,kbk

Mila: http://www.math.edu.pl/cechy-przystawania-trojkatow