Zadanie z pola czworokąta z kl 1
pm:
1. Przekątne równoległoboku o polu równym 16√2 cm2 przecinają się pod kątem, którego sinus
wynosi 2√2/3. Jedna z przekątnych tego równoległoboku jest trzykrotnie dłuższa od drugiej.
a) Uzasadnij, że krótsze boki tego równoległoboku są prostopadłe do jednej z przekątnych.
b) Oblicz obwód tego równoległoboku.
to jest to samo zadanie co
https://matematykaszkolna.pl/forum/206876.html, ale jak mam obliczyć ten diabelny bok BEZ twierdzenia cosinusów
czy sinusow ?!?! Całą resztę czaję, ale potrzbuje bardziej elementarnego rozwiązania tego
boku.
17 gru 22:25
a7:
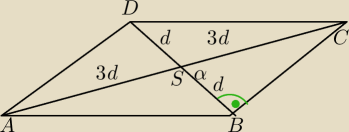
PΔABS=PΔBSC=PΔCDS=PΔADS=1/2d*3d*sinα=1/2d
2sinα=16
√2 czyli d=2 3d=6
Zakładamy że ΔBSC jest prostokątny i z Pitagorasa

liczymy BC BC=4
√2 sprawdzamy czy sinα się zgadza sinα=2
√2/3 czyli rzeczywiście kąt
SBC jest prosty
nie wiem czy tak można zrobić, ale byłby to prostszy sposób
17 gru 22:53
a7: tam oczywiście są chochliki, ale może potrafisz wychwycić lub poprawić, pytaj smiało
17 gru 22:57
a7: PΔBSC=PΔDSC gdyż sin(180−α)=sinα
17 gru 23:00
Mila:
Piszę.
17 gru 23:08
a@b:

17 gru 23:17
Mila:
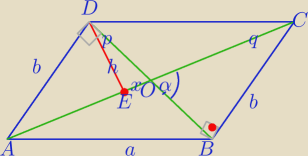
1) q=3p
p
2=16⇔p=4 i q=12
2)
|DO|=2, |AO|=6
P
BOD=4
√2
W ΔDEO:
| | 2√2 | | h | |
sinα= |
| = |
| ⇔h=U{4√2{3} |
| | 3 | | 2 | |
x
2+h
2=2
2⇔x
2+(U{4
√2{3})
2=4
| | 2 | | 2 | | 16 | |
x= |
| , |AO|=6− |
| = |
| |
| | 3 | | 3 | | 3 | |
3) W AED:
b=4
√2
| | 2 | | 20 | |
4) w ΔDEC: |EC|=6+ |
| = |
| |
| | 3 | | 3 | |
a
2=48
a=4
√3
5) W ΔAOD:
b
2+2
2=32+4=36=6
2=|AO|
2⇔
|∡ADB|=90
0=|∡CBD|
==================
17 gru 23:32
a@b:
Nieco krócej

|OE|=2/3 to |AO|=16/3 i h= 4
√2/3
jeżeli kąt ADO =90
o
to zachodzi równość h
2=|AE|*|EO|
| | 32 | | 2 | | 16 | | 32 | |
sprawdzamy: |
| = |
| * |
| = |
| |
| | 9 | | 3 | | 3 | | 3 | |
zatem kąt ADO=90
o
i dalej już z górki z pomocą Pitagorasa

17 gru 23:45
Mila:
Też myślałam o tym , jeśli chodzi chodzi o prostopadłość.
Dobranoc

17 gru 23:50
a@b:

17 gru 23:57
a@b:
Poprawię jeszcze chochlika

17 gru 23:58
 PΔABS=PΔBSC=PΔCDS=PΔADS=1/2d*3d*sinα=1/2d2sinα=16√2 czyli d=2 3d=6
Zakładamy że ΔBSC jest prostokątny i z Pitagorasa
PΔABS=PΔBSC=PΔCDS=PΔADS=1/2d*3d*sinα=1/2d2sinα=16√2 czyli d=2 3d=6
Zakładamy że ΔBSC jest prostokątny i z Pitagorasa liczymy BC BC=4√2 sprawdzamy czy sinα się zgadza sinα=2√2/3 czyli rzeczywiście kąt
SBC jest prosty
nie wiem czy tak można zrobić, ale byłby to prostszy sposób
liczymy BC BC=4√2 sprawdzamy czy sinα się zgadza sinα=2√2/3 czyli rzeczywiście kąt
SBC jest prosty
nie wiem czy tak można zrobić, ale byłby to prostszy sposób


 |OE|=2/3 to |AO|=16/3 i h= 4√2/3
jeżeli kąt ADO =90o
to zachodzi równość h2=|AE|*|EO|
|OE|=2/3 to |AO|=16/3 i h= 4√2/3
jeżeli kąt ADO =90o
to zachodzi równość h2=|AE|*|EO|



