działania na zbiorach. prawdopodobieństwo noname: Wykaż, że jeżeli P(A∩B')=0,7, to P(A'∩B)≤0,3

Blee: P(AnB') = 1 − P( (AnB')' ) = 1 − P( A' u (B')' ) = 1 − P(A' u B) <−−− na mocy prawa De Morgana tak więc: P(A'uB) = 1 − 0.7 = 0.3 P(A'nB) ≤ P(A'uB) c.n.w.

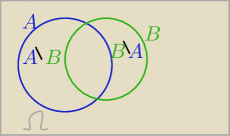
a@b: Ze schematu Venna A∩B^'=A\B i A^'∩B=B\A ( obydwie różnice są rozłączne zatem P(A∩B^')+P(A^'∩B)≤P(Ω)=1 to P(A^'∩B)≤ 1−P(A∩B^')= 1−0,7 P(A^'∩B)≤0,3 c.n.w.